Jigsaw Puzzle Orbitals
Table of Contents
- Preliminaries
- Special properties of Jigsaw Puzzle Orbitals
- Construction of Jigsaw Puzzle Orbitals*
- References and Other Resources
Preliminaries
Questaal’s basis functions consist of augmented waves : smooth envelope functions with holes punched out around atoms the smooth envelope replaced (“augmented”) by numerical solutions of the Schrodinger equation. These numerical solutions are very accurate, so basis incompleteness mostly originates from the envelope functions.† This page is concerned with a new construction for them, the Jigsaw Puzzle Orbitals.
Similar to Questaal’s traditional basis set, Jigsaw Puzzle orbitals are constructed out of smooth Hankel functions and generalised Gaussian orbitals. The reader is advised to read at least the introductory part of this documentation describing smooth Hankel functions.
Special properties of Jigsaw Puzzle Orbitals
Jigsaw Puzzle Orbitals (JPOs) have a number of highly desirable properties of a basis set.
- They are short ranged and atom centred, with pure character on the augmentation boundary where they are centred. Thus, they serve as good projectors for special subspaces, e.g. correlated atoms where the correlation is strong in a particular l channel such as transition metals and f shell metals.
- They are smooth everywhere. This greatly facilitates their practical implementation.
- They have an exponentially decaying asymptotic form far from a nucleus, making them short range.
- They are tailored to the potential. Inside or near an augmentation site, the Schrödinger equation is carried by almost entirely by a single function. Thus they form a nearly optimum basis set to solve the Schrödinger equation over a given energy window.

The solid parts depict the interstitial region, where the envelope functions carry the wave function. Dashed lines depict augmented regions where the envelope is substituted by partial waves — numerical solutions of the Schrödinger equation. It is nevertheless very useful that the envelope functions are smooth everywhere, since sharply peaked envelope functions require many plane waves to represent the smooth charge density
At points where the envelope functions and augmented functions join, the function value is unity on the head site ( or on the left, and or on the right) and zero on the other site. (By unity we refer to the radial part of the partial wave; the full wave must be multiplied by , which for p orbitals is depending on whether the point is right or left of centre.) Moreover, the kinetic energy is tailored to be continuous at the head site and vanish at the other site.
These two facts taken in combination are very important. Consider the Schrödinger equation near an augmentation point. Inside the augmentation region, the partial wave is constructed numerically, and is very accurate. It is not quite exact: the partial wave is linearized, and the potential which constructs the partial wave is taken to be the spherical average of the actual potential. But it is well established that errors are small: the LAPW method, for example, considered to be the gold standard basis set for accuracy, makes the same approximation. Since the kinetic energy is continuous across the boundary, the basis function equally well describes the Schrödinger on the other side of the boundary, at least very near the boundary.
This alone is not sufficient to make the basis set accurate. Tails in some channel from heads centred elsewhere will contribute to the eigenfunction. They can “contaminate” the accurate solution of the head. However, consider the form of the Schrödinger equation:
By construction both value and kinetic energy of all basis functions vanish except for the single partial wave that forms the head. Thus any linear combination of them will yield a nearly exact solution of the Schrödinger equation locally.
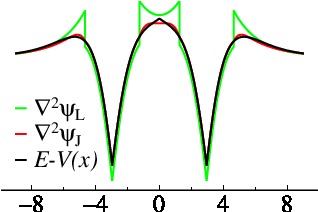 In the 1D model described above, a the JPO basis was applied to double-exponential potential well shown in black in the Figure on the right. The kinetic energy of a traditional smooth Hankel (green) shows a discontinuity at the augmentation boundary; with JPO’s the discontinuity disappears (red). The JPO kinetic energy is everywhere very close to the exact solution (the exact potential and kinetic energies lie on top of each other).
In the 1D model described above, a the JPO basis was applied to double-exponential potential well shown in black in the Figure on the right. The kinetic energy of a traditional smooth Hankel (green) shows a discontinuity at the augmentation boundary; with JPO’s the discontinuity disappears (red). The JPO kinetic energy is everywhere very close to the exact solution (the exact potential and kinetic energies lie on top of each other).
In many respects, JPOs are nearly ideal basis functions: they are close to being as compact as possible for solving the Schrödinger equation in a given energy window. JPO’s have two important drawbacks, however:
- They are complex objects, complicating their augmentation and assembling of matrix elements. We can however make use analytic properties of JPO envelope functions to greatly ameliorate the increase in computational cost in making matrix elements. The extra cost is not important provided it does not dominate the total cost.
- There is no analytic form for products of two of them, as there are for plane waves and Gaussian orbitals. However the same technology we have built for Questaal’s traditional orbitals based on smooth Hankel functions. can be applied here.
Construction of Jigsaw Puzzle Orbitals*
JPOs are tangentially related to Andersen’s tight-binding transformation and NMTO method.2 This transformation makes conventional LMTO’s short ranged (see Fig. 5 in the Questaal methods paper, Ref. 3). It makes both conventional LMTO’s and smooth Hankel functions short range in the same way, but Questaal’s functions are more accurate, shorter ranged, and suited for modern full-potential methods. NMTOs do establish proof-of-principle: they are very accurate over the relevant energy window (roughly Ry).
 To date we have succeeded in rotating Questaal’s standard basis functions (convolutions of Hankel and Gaussian functions) into a screened form; see Section 3.12 in the Questaal methods paper, Ref. 3) This basis set spans the same hilbert space as Questaal’s traditional basis — good, but not optimal.
To date we have succeeded in rotating Questaal’s standard basis functions (convolutions of Hankel and Gaussian functions) into a screened form; see Section 3.12 in the Questaal methods paper, Ref. 3) This basis set spans the same hilbert space as Questaal’s traditional basis — good, but not optimal.
The figure on the left shows screened envelope functions, , , , , and , for a zincblende lattice. They resemble a traditional Slater-Koster form (having pure character), making easy identification with an atomic orbital.
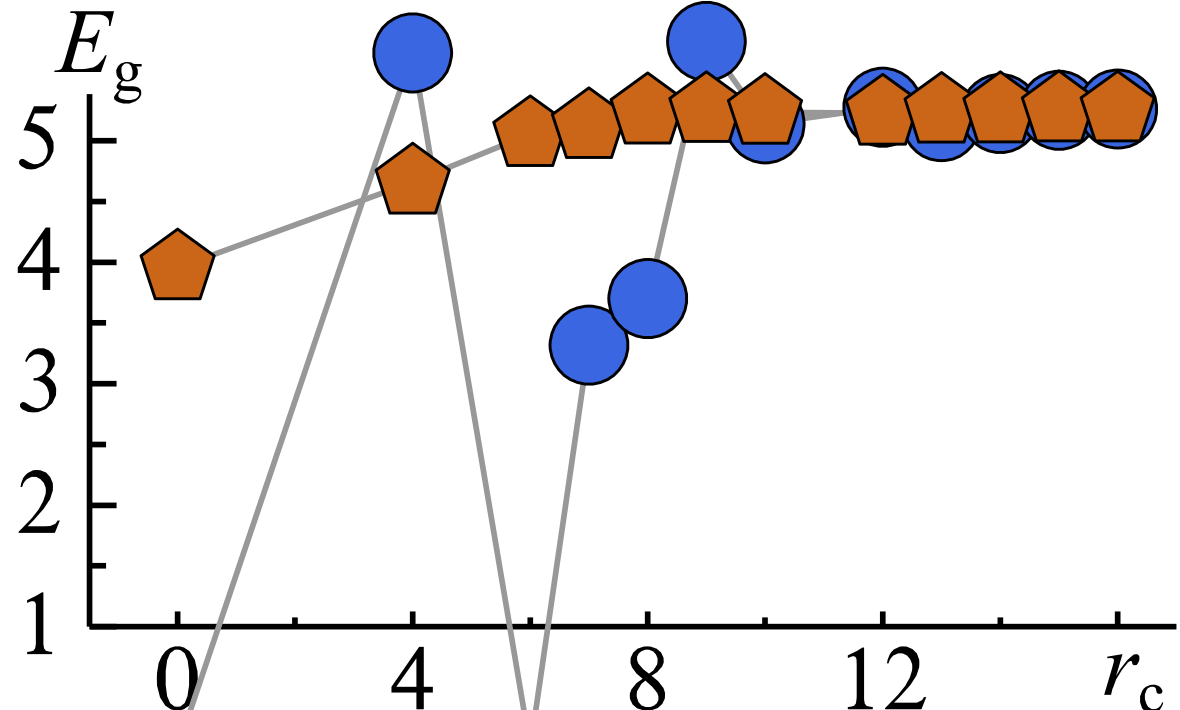 The figure on the right shows the bandgap‡ in NiO calculated in the Quasiparticle Self-Consistent GW (QSGW) approximation, comparing Questaal’s traditional basis and a screened form. The bandgap is plotted as a function of the cutoff in the QSGW self-energy for traditional envelope functions (blue) and screened basis set (orange). The first point contains onsite terms only, the second adds first neighbours etc. The conventional basis shows erratic behaviour until at least the fourth neighbours are present. JPO’s converge quickly, because their range is smaller than the range of the physical , so what the evolution of the gap is a reflection of the nonlocality in the .
The figure on the right shows the bandgap‡ in NiO calculated in the Quasiparticle Self-Consistent GW (QSGW) approximation, comparing Questaal’s traditional basis and a screened form. The bandgap is plotted as a function of the cutoff in the QSGW self-energy for traditional envelope functions (blue) and screened basis set (orange). The first point contains onsite terms only, the second adds first neighbours etc. The conventional basis shows erratic behaviour until at least the fourth neighbours are present. JPO’s converge quickly, because their range is smaller than the range of the physical , so what the evolution of the gap is a reflection of the nonlocality in the .
It is seen to be relatively short-ranged, but not confined to a single site which theories such as LDA+U and LDA+DMFT assume.
The final step, making the kinetic energy everywhere continuous, slightly perturbs the shape and should significantly improve its accuracy.
References and Other Resources
Many mathematical properties of smoothed Hankel functions and the family are described in this paper: E. Bott, M. Methfessel, W. Krabs, and P. C. Schmid, Nonsingular Hankel functions as a new basis for electronic structure calculations, J. Math. Phys. 39, 3393 (1998)
O. K. Andersen et al., “Electronic Structure and Physical Properties of Solids: The Uses of the LMTO Method,” in Lecture notes in physics, Vol. 535 (Springer-Verlag, Berlin, 2000) H. Dreysse, ed.
Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Comp. Phys. Comm. 249, 107065 (2020).
† This remark must be qualified. A basis set that is nearly perfect in describing a local potential may still be incomplete in important ways. On particularly important example arises in the context of many-body theory. A cusp appears in the two-particle wave function as , because of the singularity in the coulomb potential . Smooth functions have difficulty approximating this cusp. Treatment of forces and phonons are another context: as the nucleus moves, the basis must shift with it because the partial waves are tailored only to solve the Schrodinger equation when the nuclear potential is not displaced. These are sometimes called “Pulay” corrections.
‡ The QSGW bandgap is slightly larger than 5 eV, as shown in the original paper describing Quasiparticle Self-Consistent GW (Phys. Rev. Lett. 93}, 126406 (2004)), larger than the experimental gap of about 4.3 eV. Including ladder diagrams in W reduces this gap close to the experiment, as will be shown in a paper by Brian Cunningham and co-workers.
