Why TiSe₂ is a band insulator, not an excitonic insulator

W. Kohn was the first to propose that a semimetal could become insulating because of excitonic effects¹. The search for an excitonic insulator has been elusive, but TiSe₂ is widely thought to be an instance of one: it has a very small but positive bandgap. Moreover, ARPES measurements show “shadow bands” at room temperature where band theory says there should be none, which was taken as an marker of the excitonic nature of the bandgap.

TiSe₂ a layered diselenide compound with space group $P\bar{3}m1$. Below 200 K, it undergoes a phase transition to a charge density wave (CDW), forming a commensurate $2{\times}2{\times}2$ superlattice ($P\bar{3}c1$) of the original structure. At the transition there is a softening of the zone boundary phonon, and changes are seen in the transport properties^2,3. It is also been observed that if the CDW is suppressed by pressure⁴ or intercalation of Cu atoms⁵, (unconventional) superconductivity appears. A quantum critical point has also been observed when pressure is applied⁶. The interplay of the CDW and superconductivity has been the subject of many studies, but even at the one-particle level whether the pristine (undoped) system is a semimetal or insulator is not well understood. A proper understanding of the the origin of the one-particle spectrum is a prerequisite for understanding the superconductivity, which this work addresses. A more detailed account of this work can be found in this preprint.

An early density-functional calculation⁷ yielded the qualitative band structure of the high-symmetry $P\bar{3}m1$ phase, and found it to be (a semimetal), a “negative gap” insulator with the Ti d-like conduction band at L dipping below the Se p-like valence band maximum at Γ. DFT also predicts the CDW phase to have a negative gap.

Cazzaniga et al.⁸ considered a GW calculation as a perturbation to the LDA, and found a gap of ~XXX meV in this phase. They also reported a “Mexican hat” band structure around the Γ point. However, both the positive gap and the Mexican hat turn out to be an artifact of the G^LDAW^LDA approximation, as we have reported previously⁹. This approximation does not normally include the off-diagonal components of the self-energy Σ. As a consequence it does not change the LDA charge density, which for TiSe₂ turns out to cause the gap become negative. Also, the omission of off-diagonal matrix elements does not allow an inverted topology of the band structure to reconstruct, and this is the likely reason for the Mexican hat structure they reported. This phenomenon is present for Ge; see Fig. 6 of Ref. 10. A calculation based on the Quasiparticle Self-Consistent GW (QSGW) approximation¹¹ does not neglect the off-diagonal components Σ, and it yields a slightly negative gap as explained in some detail in Ref. 9 (see especially. Fig. 2).

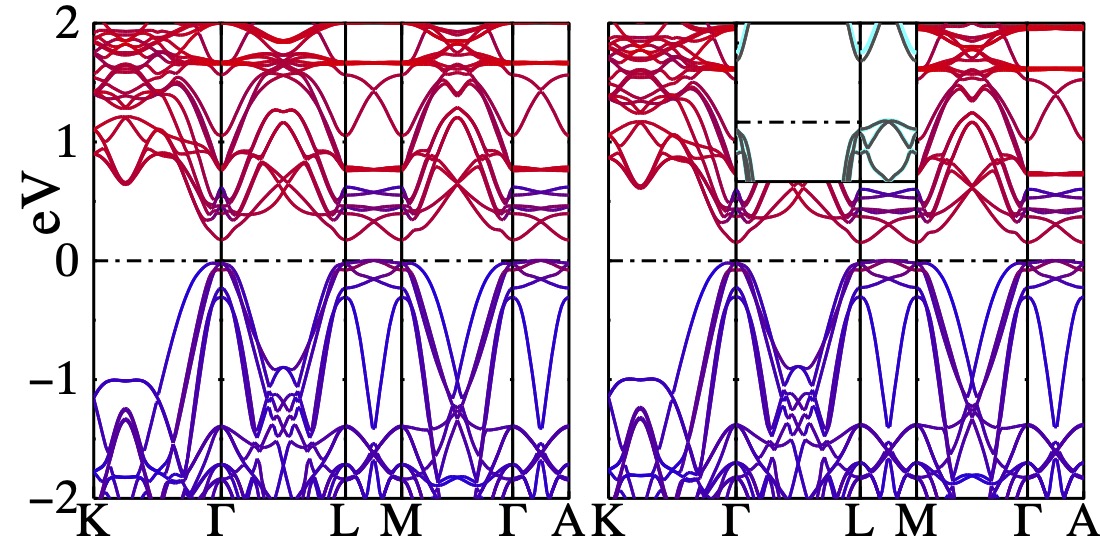
Interestingly, the QSGW bandgap is slighly positive in the CDW phase FIG 1), but slightly negative in the high-symmetry phase. Questaal’s GW algorithm can also add ladder diagrams to the polarizability¹². We call this the QSGŴ approximation, to distinguish it from QSGW, which computes W in the RPA. QSGŴ provides an ab initio way of incorporating excitonic effects, and it allows us to assess their role in the band structure of TiSe₂. As Fig. 1 shows, the difference between QSGŴ and QSGW is practically negligible; thus we can conclude with confidence that excitons play little role in the CDW phase. they play in important role in TiSe₂.

The observations can be summarized as follows:

• The CDW ($P\bar{3}c1$) phase is slight structural deformation of high-symmetry $P\bar{3}m1$ phase
• QSGW predicts the CDW to be insulating, with gap 0.17 eV, which agrees with available experiments within the resolution of the experiment.
• Incorporating excitonic effects in W (W → Ŵ) has almost negligible effect. This implies that almost certainly the CDW is a band insulator.
• At the same time QSGW predicts high-symmetry $P\bar{3}m1$ phase to be metallic, with the Ti d state at L below the Fermi level E_F.
• Numerous APRES measurements show the Ti d state at L above E_F, with a “shadow” band below it.
• Recent ARPES measurements¹³ show adiabatic change in gap across the transition temperature. This suggests the gap above 200  and below 200  have a common origin.

If we are to reconcile these seemingly contradictory observations, we must answer this question:

Is $P\bar{3}m1$ insulating because of excitonic effects, and $P\bar{3}m1$ is similar to $P\bar{3}c1$ only by coincidence? Or is there another explanation? The correct explanation must account for the contradictions between theory and experiment noted above.

The answer turns out to be conceptually simple : it is consequence of how properties are averaged.

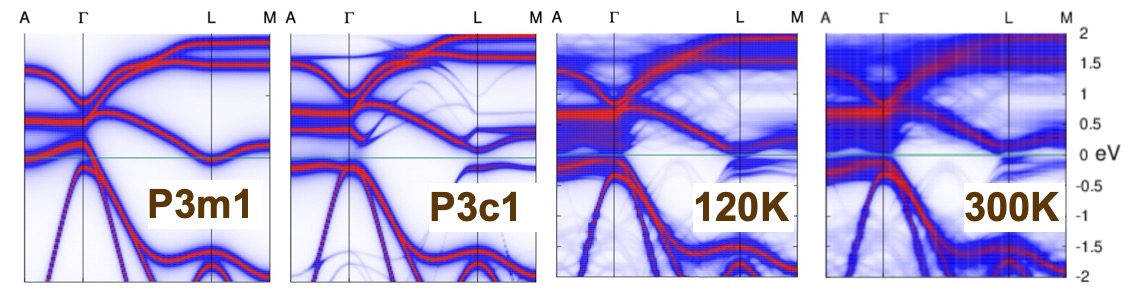
We show that while the time-averaged lattice structure assumes $P\bar{3}m1$ symmetry, the time-averaged energy band structure is closer to the CDW. To establish this, we perform ab initio molecular dynamics (AIMD) simulations on 96-atom supercells of TiSe₂, and take snapshots from the simulations far enough separated in time that they are uncorrelated. For each snapshot, we perform a QSGW calculation and obtain the energy band structure. We then unfold the Brillouin zone using a technique outlined in this tutorial, which yields a spectral function in the $P\bar{3}m1$ Brillouin zone. Finally combine the bands from all the snapshots to arrive at a time-averaged spectral function in the $P\bar{3}m1$ Brillouin zone. In the CDW and 96 atom supercells, k is no longer a good quantum number, so bands at other k points can make partial contributions to the fundamental k by what amounts to Umklapp scattering. This is no scattering in the ideal $P\bar{3}m1$ structure, so the spectral function essentially reproduces the $P\bar{3}m1$ band structure. In the $P\bar{3}c1$ phase, however, the small deformations transforming $P\bar{3}m1$ into the CDW do have Umklapp processes, and from the presepective of the $P\bar{3}m1$ Brillouin zone, the Ti 3d state at L is pushed above E_F, and also a replica of the Se valence band on the Γ-A line appears as a “shadow band” on the L-M line.

The time-averaged spectral function from the 120 K and 300 K simulations fall somewhere between the $P\bar{3}m1$ and CDW spectral functions, but they more closely resemble the CDW than the $P\bar{3}m1$, and well correspond to ARPES observations. Also, there is no dramatic diffence between the 120 K and 300 K spectra: the gap at 120 K is predicted to be 50 meV smaller than at 3000 K, in excellent agreement with ARPES¹³.

Thus we conclude that TiSe₂ is a band insulator in both low- and high temperature phases, as a result of symmetry-breaking from nuclear displacements. In the CDW, the symmetry breaking is static; in the high-temperature phase it is dynamical, and thus it is a rare instance of a metal-insulator transition induced by dynamical symmetry breaking. The final conclusion, while readily understood once obtained, is nontrivial. The followng recapitulates all the ingredients required to obtain this result:

• A GW calculation with self-consistency was essential to determine whether the ideal $P\bar{3}m1$ structure was insulating or semimetallic
• Ladder diagrams we needed to show conclusivly that excitons were not significant in the CDW phase
• AIMD simulations were needed to model the nuclear fluctations,
• QSGW calculations of AIMD snapshots were necessary to realize an accurate band structure, together with the Brillouin zone unfolding technique to average the snapshots and make it possible to interpret the bands from the perspective of the $P\bar{3}m1$ structure.

Arbitrary small deformations of the $P\bar{3}m1$ phase do not necessarily yield a gap. Remarkably, the gap persists through nearly all the snapshots used to compose the time-averaged spectral function.

References

¹ W. Kohn, Phys. Rev. Lett. 19, 439 (1967.)

² F. J. D. Salvo, D. E. Moncton, and J. V. Waszczak, Phys. Rev. B 14, 4321 (1976).

³ M. Holt, P. Zschack, H. Hong, M.-Y. Chou, and T.-C. Chiang, Phys. Rev. Lett. 86, 3799 (2001).

⁴ A. F. Kusmartseva, B. Sipos, H. Berger, L. Forro, and E. Tutis, Phys. Rev. Lett. 103, 236401 (2009).

⁵ E. Morosan et al., Nature Phys 2, 544 (2006).

⁶ Y. Joe, P. Chen, X. Ghaemi, et al., Nat. Phys. 10, 421 (2014).

⁷ A. Zunger and A. J. Freeman, Phys. Rev. B 17, 1839 (1978).

⁸ M Cazzaniga, at al, Phys. Rev. B 85, 195111 (2012)

⁹ S. Acharya, D. Pashov, A. N. Rudenko, M. Rösner, M. van Schilfgaarde, and M. I. Katsnelson, npj Comput. Mater 7, 208 (2021).

¹⁰ M. van Schilfgaarde, Takao Kotani, S. V. Faleev, Phys. Rev. B74, 245125 (2006)

¹¹ (Questaal’s methods paper) Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Comp. Phys. Comm. 249, 107065 (2020).

¹² Brian Cunningham, Myrta Gruening, Dimitar Pashov, Mark van Schilfgaarde, Phys. Rev. B 108, 165104 (2023)

¹³ Matthew Watson et al, Phys. Rev. Lett. 122, 076404 (2019).