Quasiparticle Origin of Spinons in SrCuO₂

SrCuO₂ has long been thought to be a near archetypal physical realization of a quasi one-dimensional (1D) system, exhibiting “spin charge” separation. Electron-hole excitations are thought to decay into two kinds of quasiparticles: “spinons” consisting of spin that carry no charge, and ``holons’’ that carry no spin. Such a separation emerges from the 1D Hubbard model. The primary evidence for this comes from angle resolved photoemission (ARPES) experiments, where a very flat peak in the valence bands is observed, not seen in band theory, which has been widely interpreted in terms of spin-charge separation.

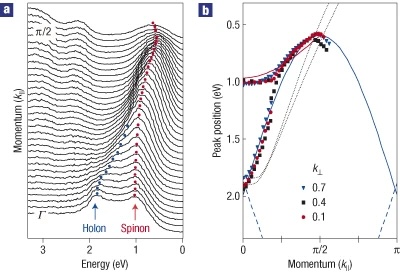Fig. 1. ARPES measurements of SrCuO₂. Right panel extracts the effective band structure from peaks in the ARPES (left). The spinon peak spans [−1.0 ,−0.7] eV; the holon peak spans [−1.9 ,−0.7] eV. Taken from Kim et al, Nature Physics 397 (2006)).

In this work we present an alternative view: we show that the canonical picture of spin-charge separation in SrCuO₂ is a one-body effect well explained in terms spin disorder. We show that ARPES, and also optical conductivity — are naturally explained in a parameter-free manner from self-consistent many-body perturbation theory (Quasiparticle Self-Consistent GW + BSE approximation), without invoking a hypothetical spin charge separation. Spinons and holons have the same quasiparticle character, the former appearing as a consequence of spin disorder. We also show that while SrCuO₂ is highly anisotropic, it is has a non-negligible 2D component, as reflected in one-particle and two-particle spectral functions. Further, we compare the features of SrCuO₂ spectral functions to La₂CuO₄ and show that the two possess many similarities, both building on a planar molecular ligand consisting of Cu in an O cage. Finally we show that the canonical view of electronic structure being localized to a single Cu + O ligands in the cuprates cannot explain the bandgap or the optics, as the Cu in its d ⁹ configuration requires at least two Cu sites.

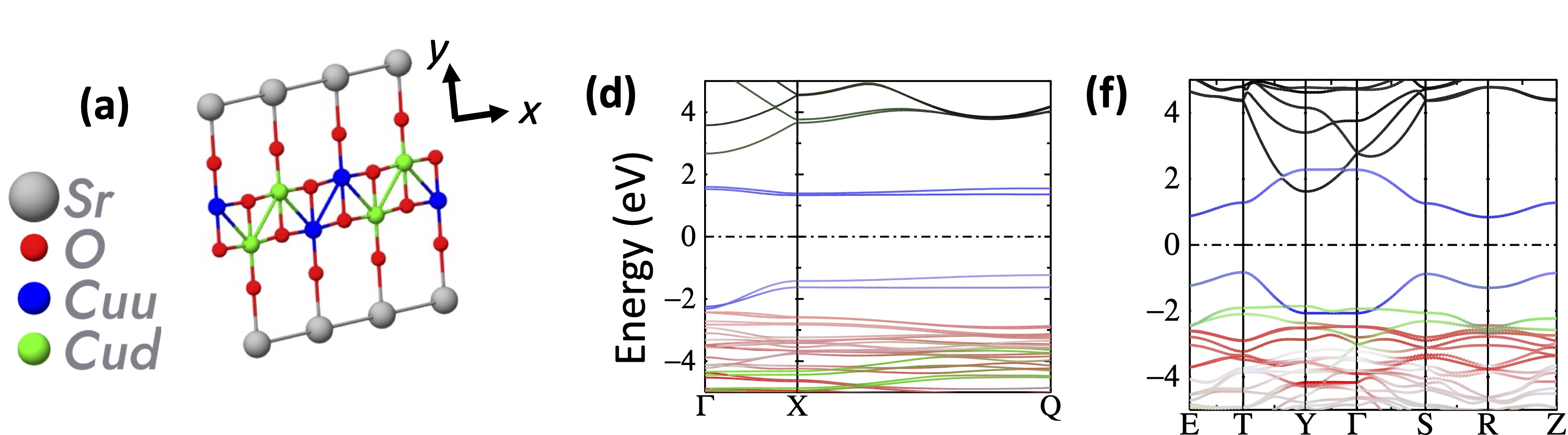Fig. 2. (a) SrCuO₂ in the minimal (16 atom) unit cell. (d,f) show the noninteracting and interacting band structure for the minimal cell in SrCuO₂ and the 14 atom cell in La₂CuO₄.

Fig. 2(d) shows the quasiparticle band structure in SrCuO₂ with the simplest spin configuration (antiferromagnetic alignment along x and ferromagnetic alignment along z). There are strong bonds along the (zigzag) chain, and weak bonds connecting chains along z. (Coupling between chains in y is very small and can be neglected here). Note the remarkable similarities with La₂CuO₄ (a 2D antiferromagnet). Colors depict orbital weights: blue, red, green project onto Cu $d_{x^2-y^2}$, $t_{2g}$, and $d_{z^2}$ character, respectively. Black depicts Sr (or La) content. In both cases the frontier (highest valence band and lowest conduction band) states have $d_{x^2-y^2}$ character, with Cu $t_{2g}$ just below. In the absence of magnetic moments, both gaps collapse. The gap forms because the $d_{x^2-y^2}$ bands have one missing electron. If adjacent Cu form bond-antibond pairs, together with a magnetic moment forming to spin-split these states, the system can arrange to have all occupied states filled, separated by a gap with unoccupied states. Dynamical Mean Field Theory can mimic this effect by allowing a single site to have both spin-up and and spin-down character, but the static picture just described fully explains the origin of the gap. That the quasiparticle picture is a truer picture of the electronic structure will be demonstrated in the description of excitons, below.

SrCuO₂ has a Neel temperature of about 4 K; thus it is disordered at room temperature. Its critical temperature is much lower than La₂CuO₄ because it is a 1D system, for which it is very difficult to sustain long range order. Neverthess it does not preclude short range order. Indeed the exchange interactions in SrCuO₂ are comparable to that of La₂CuO₄, which does sustain long range order up to approximately room temperature. Thus some short range order is expected, which complicates our ability to model the spin structure of SrCuO₂. A simple kind of disorder the preserves net 0 local moment is to double the 16-atom cell along the z axis, forming a 32 atom cell that includes chains in two distinct planes. (The planes can be aligned ferromagnetically or antiferromagnetically; there is a slight increase in the gap in the latter case. The 32 atom AFM system is the one believed to correspond to the low-temperature ordered state.) To minimally disorder the system, one spin in each chain can be flipped.

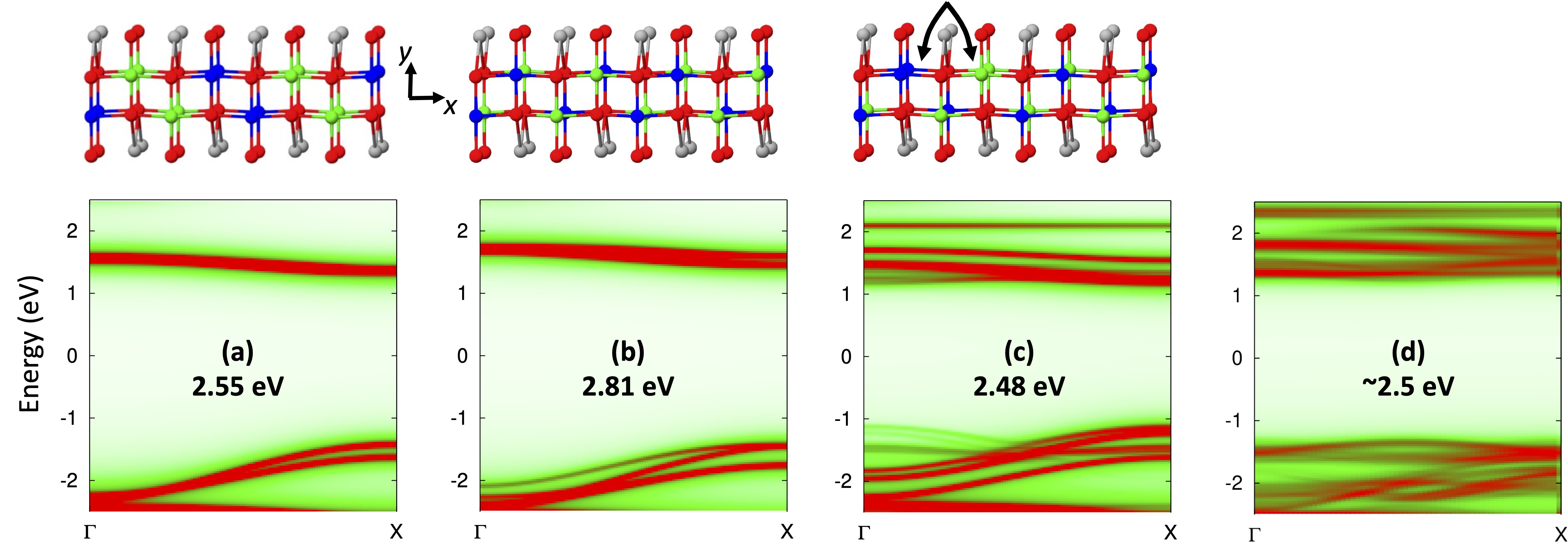Fig. 3. Spectral functions of SrCuO₂ (a) in the minimal (16 atom) unit cell, (b) in the 32 atom AFM cell; (c) in the 32 atom cell with two spins flipped; (d) configurationally averaged randomly ordered spins.

Fig. 3 shows the consequences of disorder. Panels (a) and (b) are both ordered, (a) with chains FM aligned in alternating planes, and (b) with AFM alignment. Panel (c) shows the change when one pair of spins are flipped, reflecting a slight bandgap increase. The resemblance to ARPES data (Fig. 1) is striking. Note that the “holon” band remains pretty much as before, but now “spinon” band appears naturally. Panel (d) shows the result from an average of 20 systems with randomly arranged spins. It shows a splitting into “spinons” and “holons” but the the resemblance to ARPES is rather poor. From this we conclude, first, that the “spinon” band is not a consequences of spin-charge separation, but simple spin disorder; and second, that the spins are not arranged randomly, but possess a high degree of short range order.

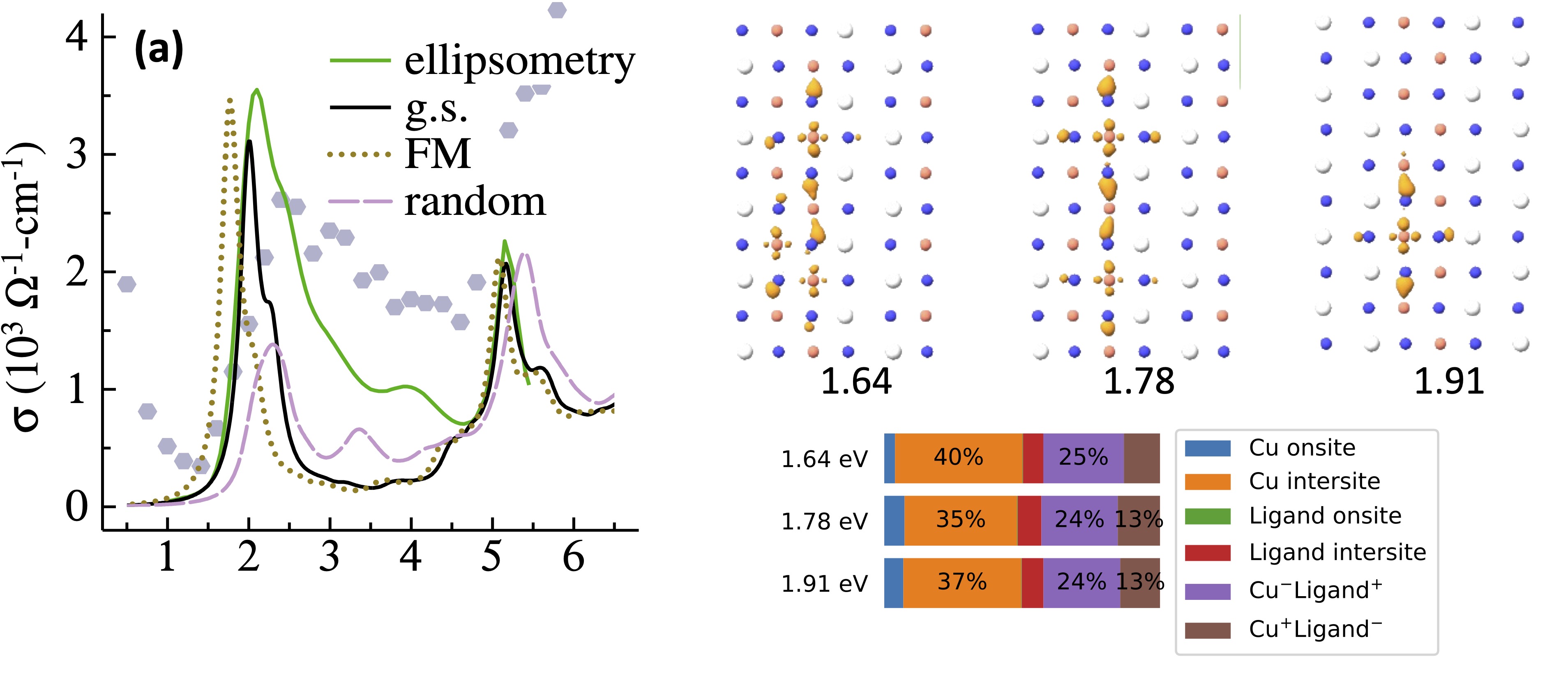Fig. 4. Optical properties of SrCuO₂. Left: conductivity $\sigma(\omega)$ as explained in the text Top right: real-space structure of three subgap excitons. Bottom: Bar chart resolving the excitons’ Mulliken decomposition into atom-atom pairs, distinguishing on-site from inter-site contributions.

The last part of the work analyzes the optical conductivity $\sigma(\omega)$, from which three important conclusions can be drawn. It is important to note that $\sigma(\omega)$ is calculated from many-body perturbation theory with ladder diagrams included via a Bethe-Saltpeter equation, and further, that the self-energy $\Sigma(\mathbf{k},\omega)$ is calculated self-consistently in many-body perturbation theory with ladder diagrams included as well. Without self-consistency, the gap would be too small; without the ladder diagrams included in W the gap would be too large.

Fig. 4 compares ellipsometry data for σ to calculations in three different spin configurations. Ellipsometry data shown in green was taken from Hilger’s PhD thesis, other measurements are similar. The dotted line was generated from the minimal 16-atom (FM) unit cell, while the black line is the 32 atomc cell with chains ordered antiferromagnetically along x (thought to be the ground state at 0 K). The pink dashed line is a configurationally averaged result from 20 random spin configurations.

The first conclusion is that $\sigma(\omega)$ is very well described by this theory, with no model or adjustable parameters. No spin-charge separation needs to be invoked. The peak in the optical gap is about 2 eV, which is 0.8  below the fundamental gap. This shows that the system has rather deep excitons, which is consistent with the weak dielectric screening expected from a quasi-1D system.

Second, dotted and black lines are the two ordered configurations, with the black one thought to correspond to the ground state configuration. The difference corresponds to two alignments of chains along x, showing that there is some hopping between the chains and that SrCuO₂ is not strictly 1D.

Third, σ for random configurations agrees far less well with ellipsometry data than σ for ordered configurations. Thus two independent markers — ARPES and σ — indicate that SrCuO₂ has a high degree of short range order.

Finally, the structure of the excitons provides very useful information about the appropriateness of widely used modely hamiltonians such as the Hubbard model. Excitons are highly anisotropic as expected, extending mostly (though not strictly) along the 1D chain, and are distributed over approximately 7 Cu sites. The distribution is important, because it indicates that the widely used, classical ligand-field description (which associates the electronic structure with a single Cu site and its ligands) does not apply here. For the same reason the Zhang-Rice (ZR) picture is inapplicable for excitons since it also assumes the single Cu site + ligand model. This point is shown in a striking way in the bar charts depicting the decomposition of the excitons into orbital pairs. In the single-Cu site model, the predominant character should be on-site (blue in the chart), corresponding to on-site d−d transitions, with some ligand character (purple and brown). Instead, the excitons are almost entirely composed of interstite transitions, either intersite Cu d−d transitions or Cu(d)−O(p) transitions.

As discussed earlier, this is a consequence of Cu being in a d ⁹ configuration. Frontier valence and conduction states have $d_{x^2-y^2}$ character (note the band edge states in Fig. 2d are blue), and the only available spin-conserving transitions between these frontier orbitals are intersite d−d transitions. The paper goes on to point out that the same argument applies to the La₂CuO₄ a 2D system and parent compound of a popular high T_c superconductor.