Band-like electron transport in amorphous In₂O₃

For an electron moving in a perfectly periodic potential, scattering is perfectly coherent. Wave functions are delocalized and characterized by a quantum number k according to Bloch’s theorem, analogous to a particle in free space, and ℏk is interpreted as the “crystal momentum.” Disruptions from periodicity by, e.g. imperfections, destroy k as a good quantum number; however if the the disruption is slight the Hamiltonian can be partitioned into a large periodic part and a weak remainder. In such a case transport can be characterized in terms of electrons propagating in states of quantum number k, with scattering between them which can be treated in perturbation theory. This is the usual description of transport in crystalline systems. If on the other hand the disorder is strong the remainder is not weak and the Bloch description breaks down. States can become localized as P.W. Andersen famously demonstrated.

Amorphous systems are the archetypal example of broken symmetry and strong disorder. They have no translational symmetry and typically exhibit poor mobility. But there are exceptions: some amorphous systems have relatively high electron mobility, for example amorphous In₂O₃. For that reason it is doped and widely used as a transparent conducting oxide (TCO) for a wide range of optoelectronic applications.

Without periodicity, Bloch’s theorem is lost, which immensely complicates our ability to characterize electronic properties. This is especially true for ab initio approaches: indeed a comprehensive first-principles description capable of evaluating electron mobility has not appeared in the literature.

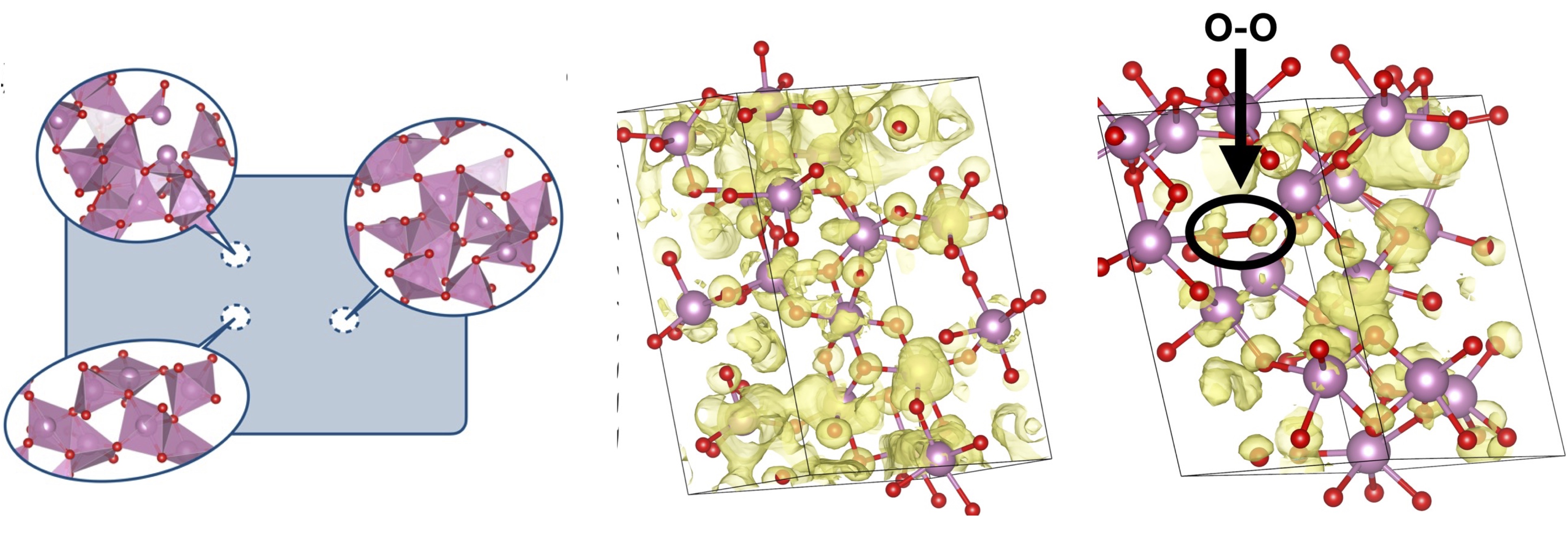Fig. 1. (Left) A schematic representation of composite of local environments. (Center) an instance of a local environment without and O-O bond. (Right) an instance of a local environment with an O-O bond.

A recent article published in Nature Physics attempts to address this issue, by employing a novel representation of the amorphous state as a statistical composite of small local environments, each of them periodic, obtained through random structure sampling. In the averaging, each environment is weighted by a Boltzmann factor, with the energy computed from density functional theory; thus the averaging depends on temperature. The theory becomes exact as the size of local environment and the number of structures both become large. In practice we used a sampling of 1500 40-atom structures. With cells of this size spatial fluctuations in the electron energies are naturally included without the need for large supercells. 40 atoms is enough to yield good accuracy while still being small enough for tractable calculations of the electronic structure based on the quasiparticle self-consistent GW (QSGW) approximation. Even 40 atoms is relatively costly at the QSGW level, so for the electronic properties we selected a randomly chosen subset of 100 structures from the original 1500.

Fig. 2. (Left) Calculated XRD intensity and configurationally averaged structure factor for a-In₂O₃, compared to available experimental data. (Right) QSGW electronic density of states is shown for both amorphous and crystalline In₂O₃ against UPS measurements.

Fig. 2 depicts structural features of a-In₂O₃ calculated in DFT: the powder XRD intensity located between q= 2-2.5 Å⁻¹ calculated from the configurationally averaged local environments corresponds well to experimental results (not shown). S(q) shows similarly good agreement. As regards electronic structure from QSGW, DOS for both c-In₂O₃ and a-In₂O₃ show good correspondence with experiment. These benchmarks establish that the composite approach provides a reasonable description of both the atomic and electronic structure.

Regarding structural differences between a-In₂O₃ and c-In₂O₃, In atoms have between 4.4 and 5.8 O atoms in the first coordination shell of In, with an ensemble average of 5.3. This indicates that the majority of In atoms are either 5- or 6-fold coordinated by O, less than the 6-fold coordination of c-In₂O₃ (called bixbyite).

To get at an effective band structure, we can compute the spherically averaged spectral function A(k,E); i.e. the probability of finding an electron with energy E and wave vector k. (Only the amplitude of k can have any meaning in an amorphous system.) For the conduction band, this is reasonable because the lowest conduction band in bixbyite is isotropic, consisting mostly of In s character.

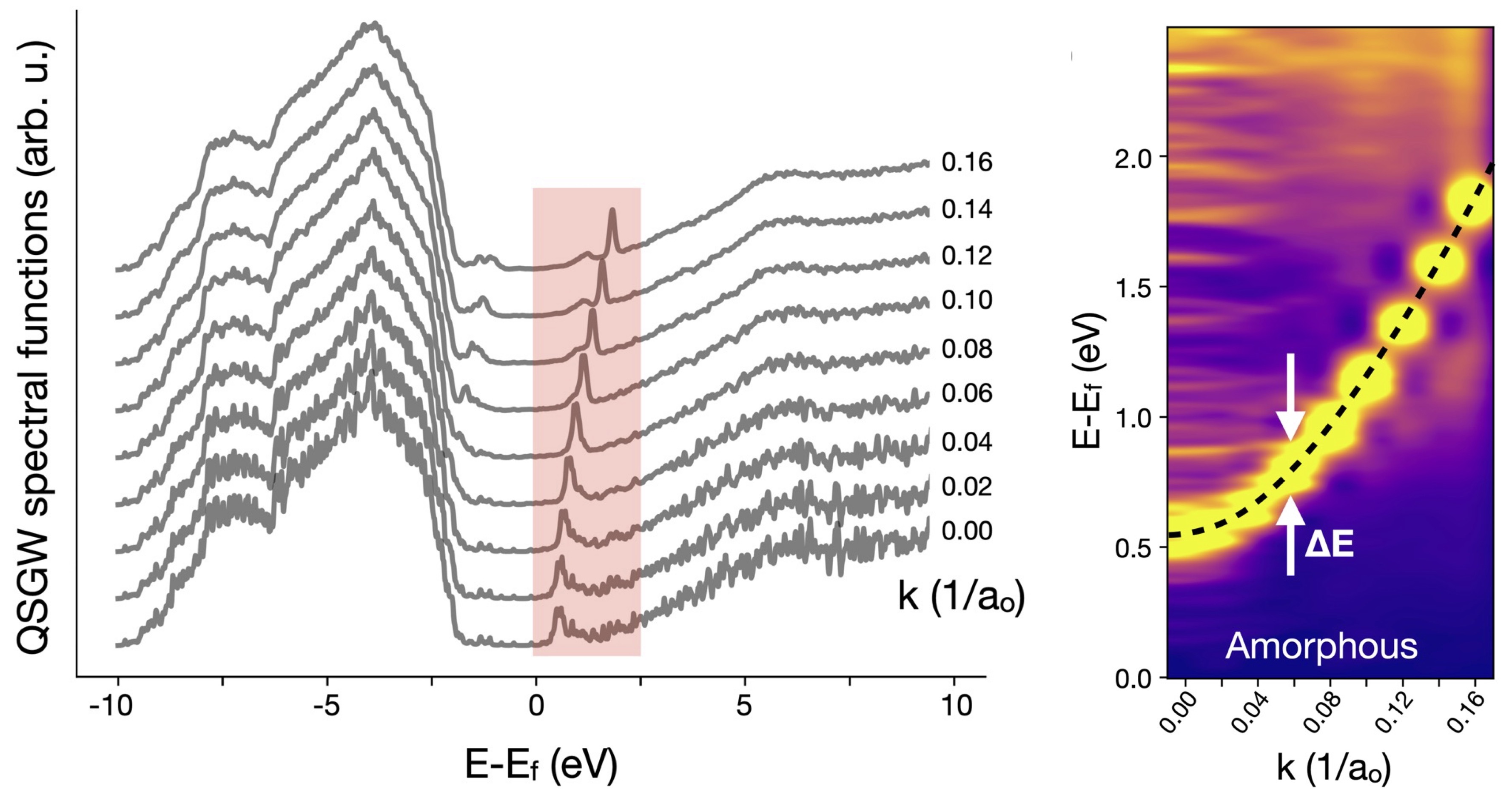Fig. 3. (Left) Configurationally averaged k-resolved spectral functions (Right) same information shown as a heat map. The dispersion E(k) is clearly visible along with the broadening.

E(k) is shown in Fig. 3. The conduction band in the shaded region has a clear peak varying as k², making it possible to extract an effective mass m^*.. The width ΔE enables us to determine the scattering lifetime and mobility standard expressions: $$\tau = \frac{\hbar/2}{\Delta E} \, , \, \mu = \frac{|e| \, \tau}{m^{*}}.$$

We find m^* ≈ 0.2 m₀, close to the m^* ≈ 0.22 m₀ the theory predicts for bixbyite. Reported experimental values range from 0.18−0.33 m₀. Near k=0, ΔE is observed to be 0.25 eV. Substituting these values in the expressions above yields an electron mobility μ ≈ 13 cm²/V-s. This is close to reported mobilities for films grown at very low temperature, but smaller than μ ≈ 60 cm²/V-s reported at room temperature growth. An explanation for the discrepancy is presented in the paper, the discussion is too involved to present here.

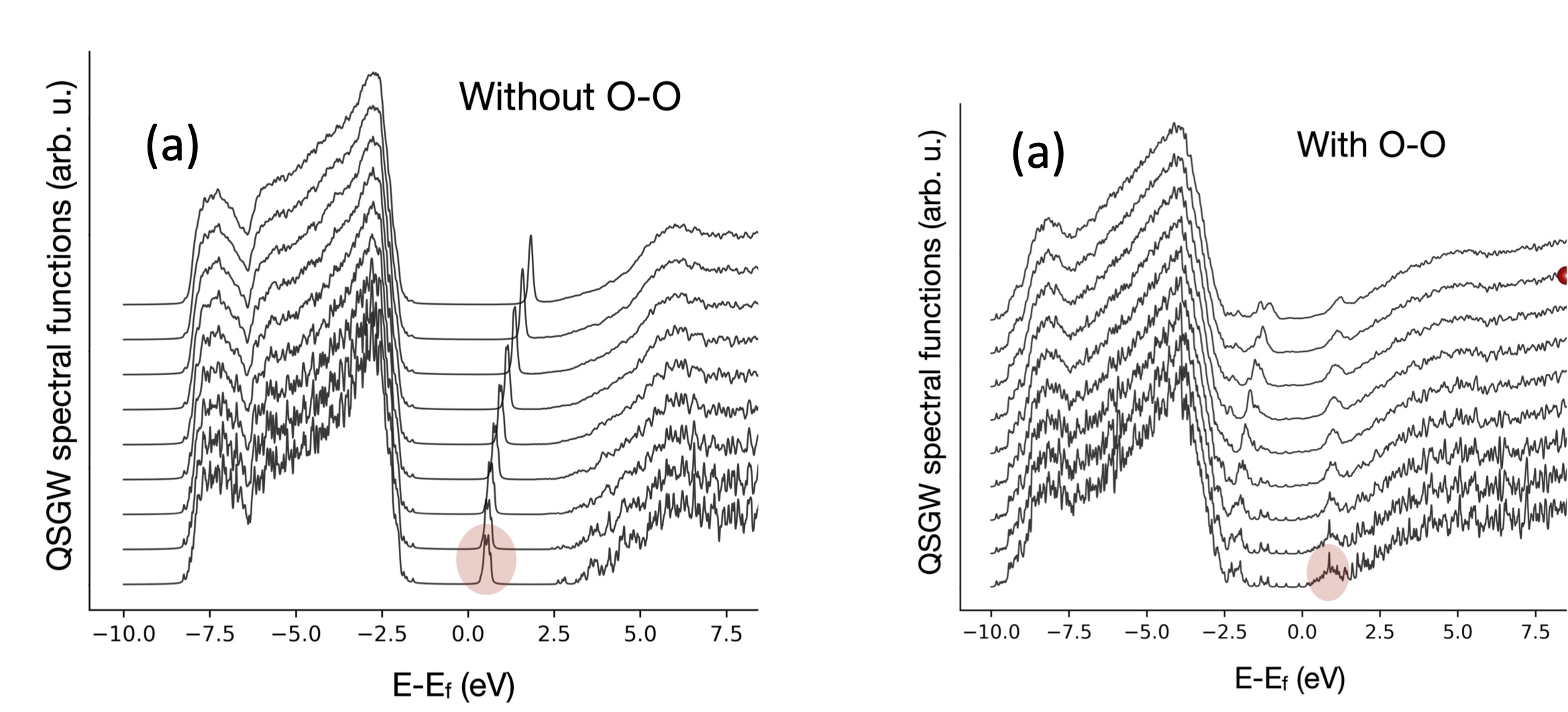Fig. 4. (Left) Dispersions in subset of structures with no O-O defects. (Right) Dispersions in subset of structures with at least one O-O defect

This study also uncovered the significant role of a defect in the form of O-O bonds. The structures were divided into those that contained no O-O bonds, and those that contained at least one. All structures without O-O defects exhibit a highly dispersive conduction band with low broadening. No midgap states are observed, and the peaks of the spectral functions in the conduction band are sharp. In contrast, if only structures with O-O bonds are considered, the dispersion breaks down and the conduction band splits into two, one set of states below the Fermi energy, and the other above (compare Figss 4a and 4b to Fig. 3a). This is primarily because the presence of an O-O bond changes the effective electron count in surrounding coordination polyhedra.