Examples
Ab initio Description of Superconductivity in Sr2RuO4
Unconventional superconductivity in Sr2RuO4 has been intensively studied for decades. Superconductivity is a quantum phenomenon where electrons participate in dissipationless charge transport. While electrons repel each other via the Coulomb force, quantum theory provides additional interactions, that in special circumstances at low temperature, can overcome the repulsion to bind electrons in Cooper pairs. Within the paradigm of unconventional superconductivity the primary glue for the Cooper pairing can originate from collective bosonic excitations other than phonons. It usually involves spin fluctuations, but a general understanding of its origin is lacking.
The origin and nature of the pairing continues to be widely debated in Sr2RuO4, in particular, the possibility of a triplet origin of Cooper pairs. It has attracted great interest because it was widely thought until very recently, that superconductivity has spin-triplet symmetry, which raises the possibility that it can sustain Majorana states conducive for topological quantum computing.
Here we employ a 4-tier ab initio theory: Quasiparticle Self-Consistent GW, Dynamical Mean Field Theory, two-particle spin and charge susceptibilities generated from the two-particle local Green’s function, and finally applying linearized Eliashberg theory with these to find instabilities to the superconducting state. We find the leading eigenvalues of both spin triplet and spin singlet superconducting states.
This work is significant for several reasons:
It is the first attempt to describe superconductivity in Sr2RuO4 ab initio, without recourse to models. More often than not, models are problematic because results are sensitive to assumptions. In the superconducting literature, this leads to endless controversy about the origins of superconductivity because the means of discriminating between model assumptions are limited. An adequately high fidelity ab initio of response functions has the potential to radically change how many-body phenomena (i.e. ones that fall outside a one-particle picture) are studied. It should be able to discriminate between models and provide real insight into the origins of many-body phenomena, and make step change in our ability to understand and predict these phenomena.
A detailed explanation for why Tc increases under tensile strain up to a critical value, and then drops off.
There is little experience telling us how well such a theory can describe superconductivity. This work benchmarks against three kinds of experiments: recent high-resolution laser ARPES measurements of the spectral function; spin susceptibility in unstrained SRO; and finally the superconducting gap function and strain-dependence of the superconducting critical temperature Tc.
As for benchmarks, Figure 1 compares a QSGW calculation of the Fermi surface to a recent laser ARPES measurement. They are nearly indistinguishable, though slight discrepancies can be seen.
The spin susceptibility for is shown in Figure 2 for three different values of strain. (the paper gives more details). The unstrained case (the only case measured to date) strong component around q=(0.3,0.3) approximately independent of . This peak is the main source of spin singlet superconductivity. A significant component near q=(0,0) also appears, which is the main source of spin triplet superconductivity. Spin susceptibility calculations agree very well with inelastic neutron measurements, although we predict the ratio of intensities near q=(0,0) and q=(0.3,0.3) to be about 1/5, somewhat larger than the observed ratio, 1/10.
Figure 3 shows the calculated gap symmetries of the three leading eigenvalues of the Eliashberg equations. As we only calculate instabilities in the normal state, not superconducting state itself, we cannot make a definite prediction about how they combine to form the superconducting state, only that the leading eigenvalues of triplet and singlet are comparable in the unstrained case.
The long-standing belief that SRO was a triplet superconductor was largely based on an observed lack of change in the Knight shift passing through Tc. Recent work has shown that very low power measurements do show a change. Also recent Quasiparticle Interference Imaging measurements of the gap function show the symmetry of a spin singlet, which looks essentially like the leading spin singlet eigenstate of Figure 3.
For details, see Communications Physics 2, 163 (2019).
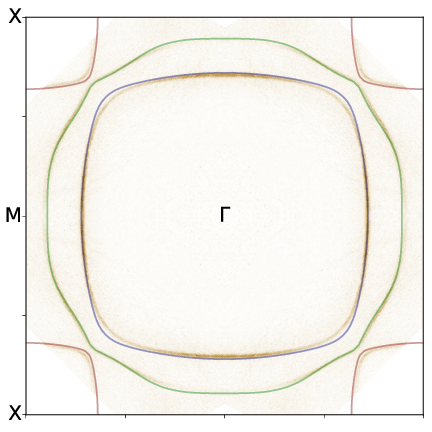
Figure 1. Fermi surface derived from Laser ARPES data in the background of a QSGW calculation of the same. Agreement is nearly perfect, though small discrepancies can be observed for the quasi-one-dimensional Fermi sheets.
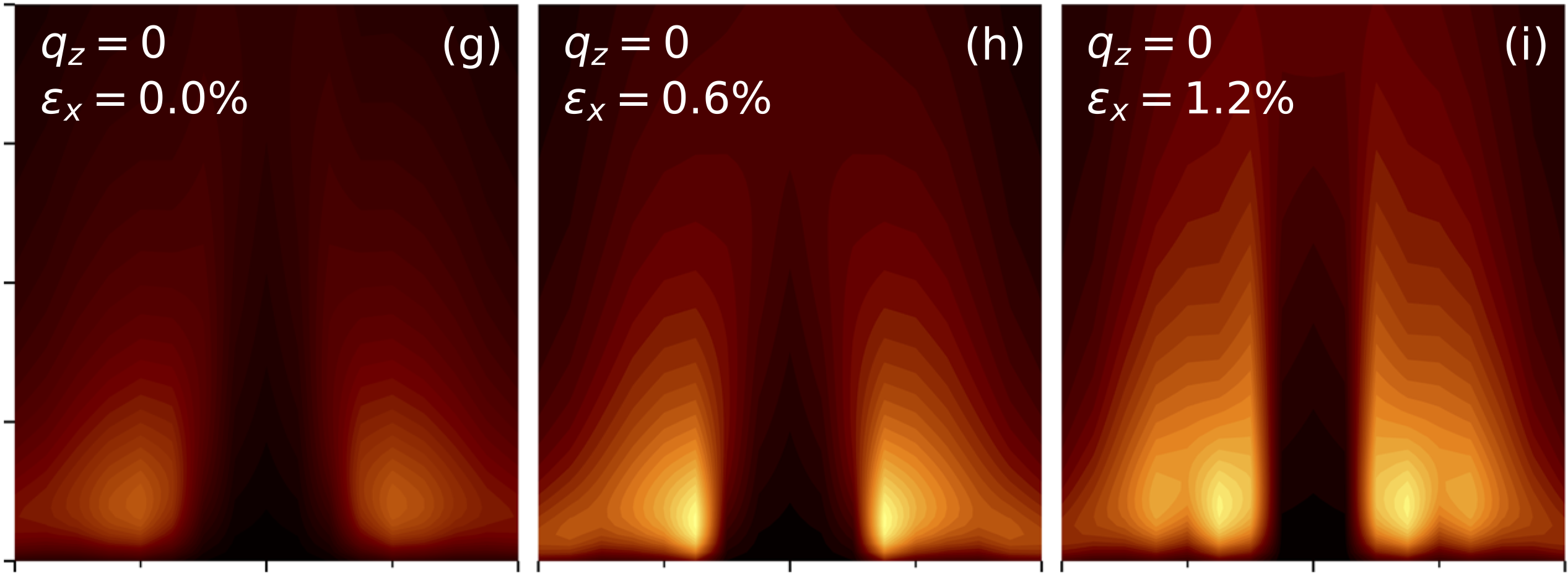
Figure 2. Imaginary part of the dynamic spin susceptibility are shown in the Cartesian xy plane for different tensile strains . The increasing sharpness of near (0.3,0.3) is the reason why Tc increases with strain. The unstrained case compares very well with INS measurements.
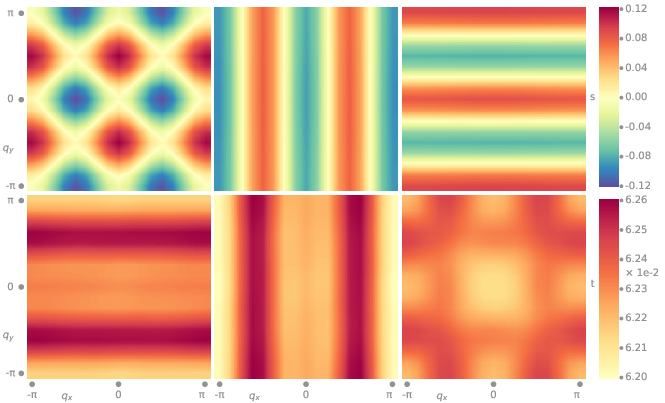 Figure 3. Superconducting pairing gap symmetries are shown in the conventional basal plane for the unstrained case. Eigenfunctions corresponding to first three eigenvalues in singlet (s) symmetries are in the top panel and triplets (t) are in the lower panel.
Figure 3. Superconducting pairing gap symmetries are shown in the conventional basal plane for the unstrained case. Eigenfunctions corresponding to first three eigenvalues in singlet (s) symmetries are in the top panel and triplets (t) are in the lower panel.
PAPERS · QSGW, DMFT, BSE · SUPERCONDUCTIVITY
