Questaal Methods Paper

This paper, published in Computer Physics Communications summarises the theory and functionality behind the Questaal package documented here. Non-commercial users are free to use this code; if you disseminate results generated by Questaal codes for any purpose, please refer to the Computer Physics Communications paper:

Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Comp. Phys. Comm. 249, 107065 (2020).

Questaal is a suite of codes for calculating the electronic structure and related properties of materials from first principles. The simplest implementation of ab initio electronic structure is the ever-popular density functional theory (DFT), for which in excess of 10,000 papers are published every year. Questaal has a standard implementation, and three simplified implementations which rely on the Atomic Spheres approximation, which bears some relation to the Muffin-Tin approximation. Among these are a band code, which had one of the first DFT implementations of noncollinear magnetism, used, for example to explain the Invar effect in Fe-Ni alloys, a crystal Green’s function code, and a layer Green’s function code designed for layered geometries.

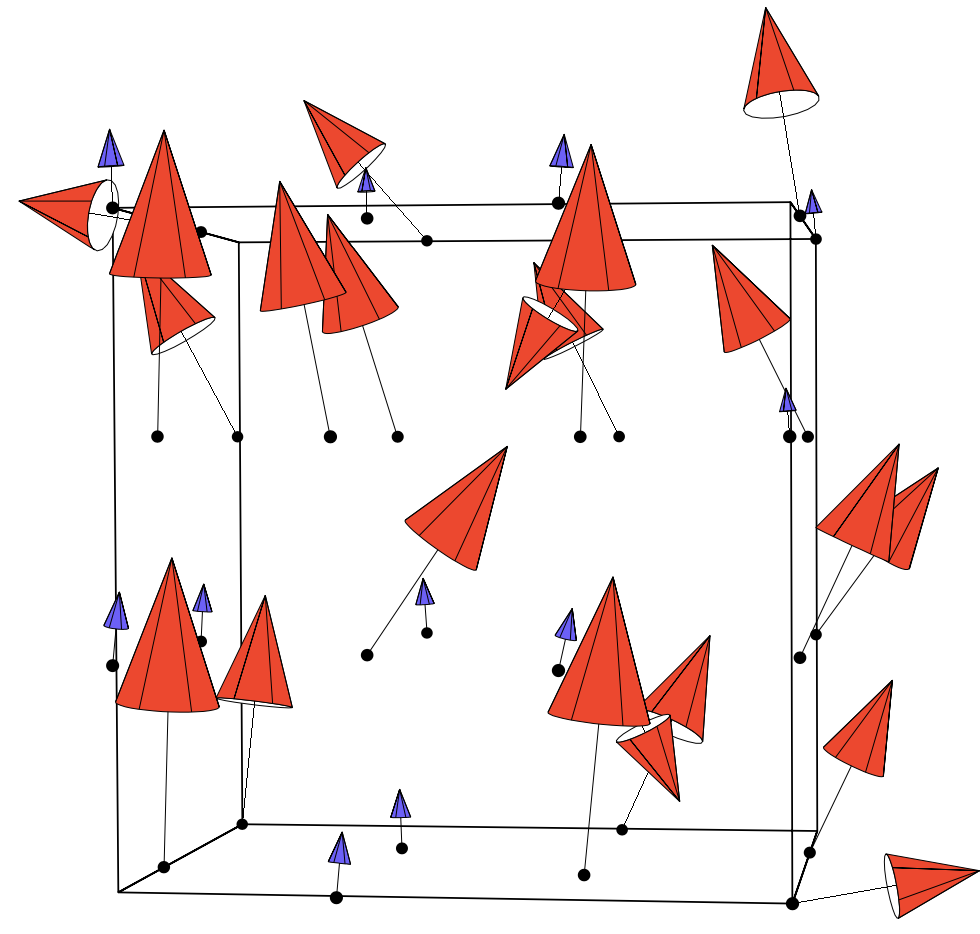
Fig 1 (left) Transition from collinear to noncollinear state in INVAR. From Nature (1999).

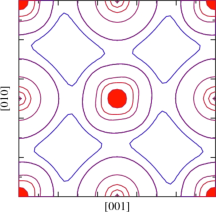
Fig 2 (right) Contours of charge density in CoO calculated from QSGW. The slight eccentricity in the density around the Co atom (center) is missed in DFT.

The former is useful for its implementation of the Coherent potential approximation and its ability to determine magnetic exchange interactions by the celebrated Lichtenstein formula; latter has the the ability to calculate transport in the framework of Landauer Buttiker theory, both equilibrium and nonequilibrium transport.

The entire Questaal suite has a large number of executables that perform different functions. A summary of the main ones can be found here.

Questaal is a descendent the LMTO methodology formulated by O.K. Andersen and his group in Stuttgart, mostly in the 1980’s. The linearised muffin-tin orbital (LMTO) formalism is revisited in detail and developed further by the introduction of short-ranged tight-binding basis functions for full-potential calculations.

A key feature of Questaal is its ability to go beyond DFT. It was the code where the Quasiparticle Self-Consistent GW approximation was first implemented, and it continues to be the best code for this theory in solids. QSGW is a special form of Hedin’s GW approximation, where self-consistency is used to build an optimal starting point for the perturbative potential, iGW. As this paper shows, self-consistency dramatically improves on the reliability and uniformity of the GW approximation. The fact that it does not rely on DFT greatly improves on the systematics of the theory. It also gives access to the ground state density and magnetic moment, which the usual DFT-GW cannot do (see Fig. 2)

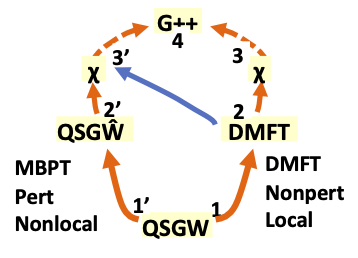
Fig 3. Questaal's two tracks for many-body perturbation theory.

QSGW does very well for charge fluctuations, but much less well for spin fluctuations. They tend to be much lower in energy: a typical energy scale for the fundamental many-body charge fluctuation (plasmon) is 1-10 eV, while the important energy scales in spin fluctuations that, for example, drive unconventional superconductivity, are in the 5-200 meV range. In such a case low-order many-body perturbation theory is inadequate, as many diagrams are needed to capture the large number of competing low-energy fluctuations. Questaal as a unique ability to combine QSGW with Dynamical Mean Field theory which includes all local diagrams, embedding a set of localised orbitals in a mean-field host. In Questaal's context, the host can be either DFT or QSGW.

DMFT brings other important advantages. Making the two-particle Green's function is tractable (though expensive), whiles yields vertices that enter into susceptibilities. It is a temperature-dependent theory, and for important many-body effects, the temperature dependence (particularly in the vertices) can be very important. It is also possible to keep all three frequency components (two fermionic frequencies and one bosonic frequency), which can be very important.

 

Fig. 4. Spin susceptibility in La₂CuO₄ centered at the antiferromagnetic vector (1/2,1/2) in units of 2π/a, at low temperature. Particularly of note are the intense peak at 5-10 meV, and paramagnon branches that stellate from (1/2,1/2) above 60 meV. It fairly well reproduces neutron measurements.

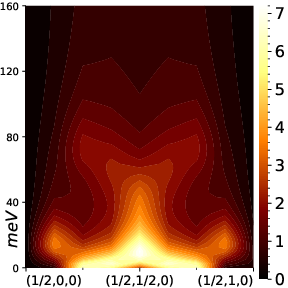
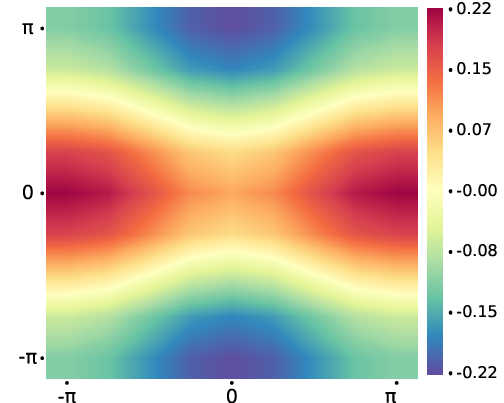
Fig. 5. Nodal superconducting gap structure for the hole-doped La₂CuO₄ showing d_{x²-y²} gap symmetry. The color bar shows the negative (in blue) and positive (in red) superconducting gap magnitudes in arbitrary units passing through node where the gap closes (in yellow).

Also, the particle-particle vertex can be derived from the particle-hole vertex generated for the susceptibilities: the objects that enter into Eliashberg theory. This makes it possible to calculate the instability to superconductivity, along with the pairing gap potential.

There is good reason to believe Questaal is an optimal vehicle for future developments in electronic structure. This is in part because of its advanced implementation of many-body theory, that does not rely on DFT, and in part because of a construction of a new basis of jigsaw puzzle orbitals that allows it to be simultaneously very accurate and very short range. An argument for Questaal as an ideal vehicle for the next generation electronic structure methods is taken up in a psi-k highlight.