Origins of Superconductivity in LaFe₂As₂ and CaFe₂As₂

Iron-based superconductors belong to a relatively newer group of “unconventional” or “high temperature” superconductors, which have high $T_c$ relative to their conventional counterparts. Iron forms compounds with arsenic (a pnictide) or selenium or tellurium (chalcogenides). These iron-based superconductors (IBS) form an important group among the unconventional superconductors. In the original explanation of Bardeen, Cooper and Schrieffer, the “glue” that mediated electrons were quantized lattice vibrations (phonons). For unconventional superconductors the glue is different, but a three decade-long effort gone into understanding them met with very limited success, particularly in the IBS family.

In a recent paper (Phys. Rev. Lett. 124, 237001) we examined a pair of configurations in two different compounds, LaFe₂As₂ and CaFe₂As₂. Each can exist in a “collapsed phase” (small c/a) and an “uncollapsed phase” (large c/a). Recent observations of selective emergence (suppression) of superconductivity in the uncollapsed (collapsed) tetragonal phase of LaFe₂As₂ has rekindled interest in understanding what features of the band structure control the superconducting T_c. In typical IBS, three states (d_xz, d_yz, and d_xy) are the important ones at E_F. Since their discovery, the prevailing view has been that d_xz+d_yz are the primary drivers of UCS. So much so that a recent paper¹ took note of the important role of d_xy in LaFe₂As₂, highlighting it as a special case differing from “traditional pnictides.” In this view, La plays the role as dopant and d_xy acts as a proxy for the usual d_xz+yz.

In this paper we perform a QSGW⁺⁺ calculation to address this question. QSGW+DMFT is extended by solving a Bethe-Salpeter equation to yield the essential two-particle objects, the spin and charge susceptibilities χ^m and χ^d. These are physical observables which themselves provide an important benchmark against experiment and offer hints as to the origins of superconductivity. Further, they supply ingredients needed for the quantities entering into the Eliashberg equation, which describes instabilities to superconductivity. QSGW⁺⁺ is a shorthand for the four-tier QSGW+DMFT+BSE+Eliashberg theory.

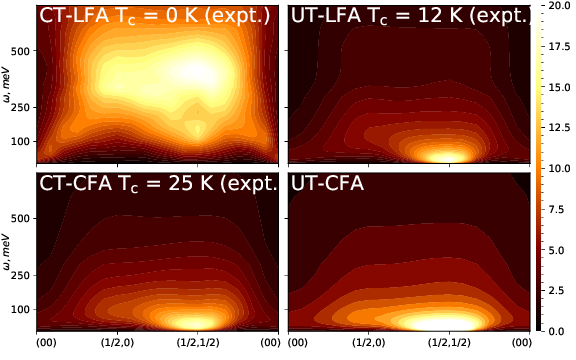
Figure 1. (From left to right) energy and momentum resolved spin susceptibility Im$\chi^m(q,\omega)$ shown for the CT and UT phases respectively. The q-path is chosen along (0,0)-$(\frac{1}{2},0$)-($\frac{1}{2},\frac{1}{2}$)-(0,0). A wide energy window was chosen to stress the absence of low energy glue in CT-LFA phase, and its nearly band like spin excitation character. The intensity in the CT phases are multiplied by five to render them comparable to the UT phases. CT-LFA (upper left) has a peak intensity around the antiferromagnetic wave vector q=(1/2, 1/2, 0), and ω>500 meV. In the other three cases this peak occurs at much smaller energy, ω∼10 meV. 50 meV is already too large an energy scale to provide glue for superconductivity, and the largest eigenvalue obtained by solving the Eliashberg equation is very small (Fig. 2).

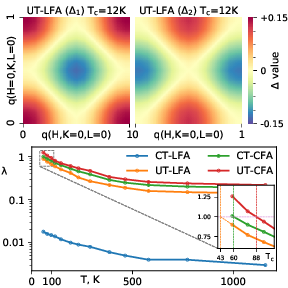
Figure 2. Two dominant eigenmodes are found by solving the Eliashberg equation, with the leading eigenvalue showing extended s-wave character, and the lagging one a d-wave. T_c occurs when the leading eigenvalue $\lambda$ from the Eliashberg equation crosses unity. CT-CFA, UT-CFA and UT-LFA are all superconducting with $T_{c}^\mathrm{UT-CFA}{>}T_{c}^\mathrm{CT-CFA}{>}T_{c}^\mathrm{UT-LFA}$, while CT-LFA has no instability. Bottom panel shows the leading ($\Delta_1$) and lagging ($\Delta_2$) eigenfunctions of the superconducting gap potential in UT-LFA.

The QSGW⁺⁺ picture is more nuanced than the view of Ref. 1. d_xy does indeed drive superconductivity: the theory correctly predicts T_c^CT−CFA>T_c^UT−LFA. When QSGW is augmented by DMFT, Hundness causes the d_xy to become very flat (the d_xz+yz much less so). This drives incoherence in the spectral function, which when combined with the proximity of d_xy to E_F is responsible for the structure of χ^m. The intense peak at small but positive ω drives superconductivity, provided it occurs at small enough ω, but not so strongly peaked near the point [q=(1/2,1/2,0),ω=0] that the superconducting instability is overtaken an antiferromagnetic one.

In the uncollapsed phase d_xy is at the Fermi energy. It is most strongly correlated of the d states and the source of enhanced scattering in both single and two particle channels. The resulting intense and broad low energy spin fluctuations suppress magnetic ordering and simultaneously provide glue for Cooper pair formation. In the collapsed tetragonal phase, the d_xy state is driven far below the Fermi energy, which suppresses the low-energy scattering and blocks superconductivity. A similar source of broad spin excitation appears in uncollapsed and collapsed phases of CaFe₂As₂. However, the antiferromagnetic instability in the uncollapsed phase is stronger than the superconducting one and overtakes it; thus it is antiferromagnetic rather than superconducting.

The QSGW⁺⁺ picture bears some similarities to Ref.1, but the crucial difference is the orbital-selective renormalization of d_xy bandwidth, which points to “Hundness.” Knowing which paradigm is correct is key to understanding unconventional superconductivity. QSGW⁺⁺ tells us a priori what the picture is, with a minimum of assumptions or reference to models. Practically, it suggests controlling coherence provides a way to engineer T_c in unconventional superconductors primarily mediated through spin fluctuations.

Strong evidence for the Hund picture can be found in an extremely informative experimental survey of IBS, Ref. 2. They correlated many observables with T_c, among them the bandwidth of d_xy, and they showed a strong correlation between it and T_c. Yet their evidence also suggests Hundness is not a universal driving force: other orbitals may play a more prominent role when d_xy is more similar to d_xz+yz.

¹ I. I. Mazin, Makoto Shimizu, Nayuta Takemori, and Harald O. Jeschke, “Novel Fe-Based Superconductor LaFe₂As₂ in Comparison with Traditional Pnictides,” Phys. Rev. Lett. 123, 267001 (2019).

² Yi, M., Zhang, Y., Shen, Z. et al. “Role of the orbital degree of freedom in iron-based superconductors,” npj Quant Mater, 2 (2017) 57.