First-principles supercurrent calculations in realistic magnetic Josephson junctions

The transport properties of superconductor-ferromagnet-superconductor (SFS) junctions have been of great importance to the scientific community for many years with increasing recent technological interests.

Since the prediction and subsequent observation of the Josephson effect some 50 years ago, the Josephson junctions (JJ) have been used for important applications in quantum circuits for metrology, quantum sensing and quantum information processing.

Conventional JJs are made of two superconductors (S) connected via a ``weak link’’ which can be either an insulator, or a normal metal (N), or a constriction. By using magnetic materials to connect the two superconductors , i.e. building a magnetic Josephson junction (MJJ), new fields of fundamental and applied research were developed. The physics of the transport properties through MJJ is fundamentally changed when the spin degeneracy of the electrons in the central region (connected the superconductors) is lifted.

At a microscopic level, the supercurrent through a short SNS junction is determined by bound states forming in the constriction due to Andreev reflection at the NS interfaces. In the Andreev reflection process, an incident electron-like quasiparticle with spin $\uparrow$ gets reflected at the NS interface as a hole-like quasiparticle with spin $\downarrow$ and a Cooper pair is emitted into the condensate. Such a process occurs at both left SN and right NS interfaces, leading to an effective transfer of Cooper pairs between the left and right superconductors, i.e. the establishment of a supercurrent in the junction. When time-reversal symmetry is not broken, electrons and holes propagate with the same velocity in the normal region. In this case, there is no phase shift accumulation between this pair of quasiparticles along their trajectories in the N region, and the sign of the critical current I_c is fixed. When I_c > 0, one talks about 0-junction.

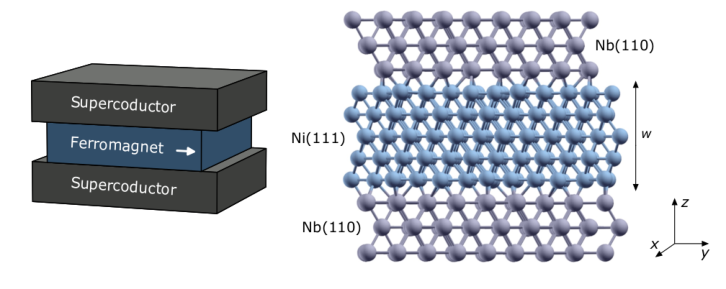FIG 1: (Left) Schematic view of a SFS junction. Arrows indicate possible magnetization of ferromagnets. (Right) Atomic representation of the Nb(110)/Ni(111)/Nb(110) junction with 5 layers of Ni. Nb atoms are light grey, Ni atoms are blue. The top and bottom atomic planes of Nb(110) are repeated periodically in the $z$-direction to create the semi-infinite Nb leads of the junction through which the current flows. Periodic boundary conditions are used in the $xy$-plane. The corresponding reciprocal space defines two-dimensional $k_\parallel$ vectors, i.e. the transverse modes, used in the calculations. —

In a MJJ, the exchange splitting in the magnetic material breaks the time- reversal symmetry and leads to an interesting interplay between superconductivity and magnetism. In SFS junctions, the correlated quasi-particles and quasi-holes forming Andreev bound states propagate through the junction under the exchange field of the ferromagnet. In many ferromagnets, such as Fe or Ni, the exchange splitting is large and, consequently, significant modifications of the Fermi surfaces and velocities of minority (spin $\downarrow$) and majority (spin $\uparrow$) carriers occur. Strong time-reversal symmetry breaking leads to the appearance of characteristic superconducting correlations with oscillatory dependence determined by the difference in wave numbers $k_F^\uparrow - k_F^\downarrow$. This effect opens the possibility for the supercurrent reversal (I_c < 0) as a function of the thickness of the ferromagnetic region, i.e. the so-called Josephson $\pi$-junction.

By increasing the thickness of the ferromagnetic layer, one gets an oscillation between the 0-junction and $\pi$-junction. The correlation between the phase shift of the supercurrent and the magnetization provides a possibility for realizing magnetic spin valves which may have promising novel applications for cryogenic superconducting digital technologies.

Working with a team at Station Q (Microsoft Quantum, Santa Barbara), we have developed a new approach to calculate the supercurrent in realistic inhomogeneous three-dimensional models of magnetic Josephson junctions. Our technique combines density functional theory with Questaal in order to capture realistic material band structure effects and a Bogoliubov-de Gennes approach for the subsequent calculations of the supercurrent. This method allows one to predict and explain key properties of magnetic Josephson junctions.

In a recent paper, we have shown that the exponential supercurrent decay, typically associated with disorder in the junction, occurs in clean systems with a complex band-structure and we have identified two mechanisms responsible for it. We also obtain an excellent agreement between our`simulations and published experimental data for the half-period of the critical current oscillations.

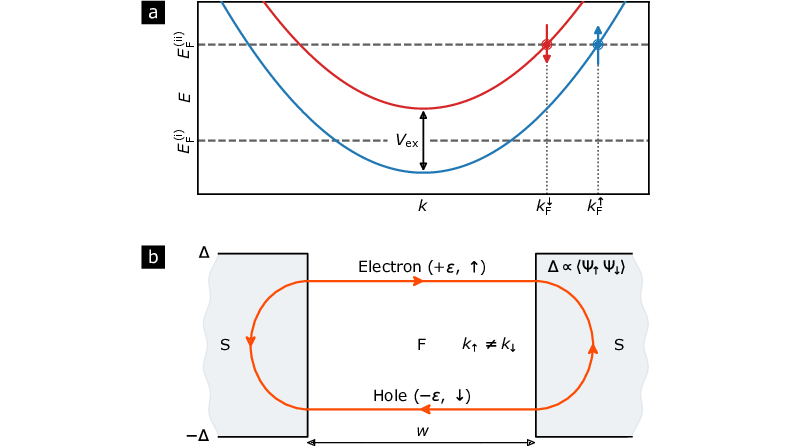FIG 2: (a) Simplified band structure of a ferromagnet, with majority and minority bands split by $V_{ex}$. $k_F^\uparrow$ and $k_F^\downarrow$ are the Fermi momenta for majority and minority carriers, respectively. The Fermi level $E_F^{(ii)}$ corresponds to small $V_{ex}$. $E_F^{(i)}$ corresponds to large $V_{ex}$, where the minority band is pushed above $E_F^{(i)}$. Thus, the propagation of minority quasiparticles is characterized by an imaginary momentum $k_F^\downarrow$ and is suppressed. For realistic band structures, the band dispersion is not parabolic, and more bands with different characters ($s, p$ or $d$) cross the Fermi level. Furthermore, there are asymmetries in the structure of the Fermi surface. For certain bands and momenta $k_\parallel$, the Fermi surface present in one spin channel may be absent in the other. And the Fermi velocity $v_z$ in the transport direction is also strongly dependent on the transverse momentum $k_\parallel$. (b) The supercurrent in a SFS junction is carried by Andreev bound states localized in the junction. The solid red line represents a quasi-classical trajectory corresponding to an Andreev bound state. The spectrum of Andreev states (from which the supercurrent is calculated) depends on the relative superconducting phase difference $\phi$ across the junction as well as the phase, $\delta\phi = (k_F^\uparrow - k_F^\downarrow)w/2$, accumulated due to the difference of Fermi momenta for majority and minority carriers. Note that in scenario (i), the propagation of minority carriers is suppressed leading to an overall exponential decay of the supercurrent with $w$. This is to be contrasted with the normal transport through the junction. —

In order to demonstrate the capabilities of the method, we considered Nb/Ni/Nb junctions. Such Nb/Ni/Nb junctions are suitable systems for comparison between simulations and experiments because of the long mean free path in Ni relative to the junction thickness and the quasi-ballistic nature of quasiparticle propagation in the ferromagnet.

FIG 3: (Top) Supercurrent $J_1$ as a function of junction thickness $w$. Full black circles correspond to $J_1$ calculated with 290 $k_\parallel$-points, empty circles (mostly superposed onto the full black circles) correspond to 4142 $k_\parallel$-points. Solid black line is a fit. Green semitransparent dashes show the different contributions to the supercurrent for the individual $k_\parallel$-points. The vertical `errorbars’ correspond to the standard deviation of each $k_\parallel$ contribution. The standard deviation is the same for both sets of $k_\parallel$-point indicating that these results are independent of the chosen discretization. (Bottom) Panel (b) shows the normal state conductance per unit of area as a function of w for majority ($G_\uparrow$) and minority ($G_\downarrow$) spins as well as the total conductance $G$. The conductance does not depend on $w$ as should be the case for metallic systems without disorder. Panels (c-e) shows the supercurrent as a function of the superconducting phase difference $\phi$ across the junction. Panel (c): for 4 atomic layers of Ni, the MJJ is in a strong 0-junction regime. Panel (e): for 13 layers of Ni, the MJJ is in a strong $\pi$-junction regime. Panel (d): for 8 layers, the MJJ is in an intermediate regime. In the 0- and $\pi$-junction regimes, the first harmonic $J_1$ of the supercurrent dominates. In the intermediate regime higher-order terms may prevail. —

The results obtained using this method have a broad impact on understanding the physics of SFS junctions. Indeed, we have identified two generic mechanisms for the decay of the supercurrent with the width of the ferromagnetic region: (a) exchange-splitting induced gap opening for minority or majority carriers and (b) dephasing between different modes due to the significant quasiparticle velocity dispersion with the transverse momentum.

It was previously believed that disorder in the ferromagnet was mainly responsible for the supercurrent exponential decay in SFS junctions as a function of width. Our work shows, for the first time, that band structure effects (for realistic systems) are also contributing to the critical current suppression and thus provide an upper bound for the supercurrent in ideal (i.e. disorder-free) structures.

Our approach opens a path for material composition and geometry optimization in magnetic Josephson junctions and superconducting magnetic spin valves, and for engineering devices with desired superconducting properties.