First principles vs second principles description of strongly correlated systems

First-principles approaches have been successful in solving many-body Hamiltonians for real materials when correlations are weak or moderate. For strongly correlated systems, model Hamiltonians (especially the Hubbard model) are widely used. They are ubiquitous because of their relative simplicity: the essential features of a physical phenomenon of interest can be elucidated without the encumbrances and unnecessary details a “first principles” approach entail, making it much easier to identify key parameters in the model which govern the property of interest. Not least, model Hamiltonians are more tractable, which greatly facilitates extracting physical observables.

Models such as the Hubbard Hamiltonian do indeed contain, within some region of parameter space, key many-body effects such as the metal-insulator transition, pseudogap phases, quantum criticality, and both conventional and unconventional superconductivity. Thus, applications of this model has become the canonical approach to characterizing such phenomena. However, its limits become apparent when the high-energy scales that control parameters for the low- energy ones are nontrivial. High-energy scales contain information about chemistry and disorder specific to real materials: they have a marked effect on the low-energy scales and cannot be integrated out without model assumptions. First principles theories in principle contain this information, and can potentially distinguish which models are applicable, and the significance of the physical mechanisms they omit.

Yet their application to strongly correlated systems has been limited. In weakly correlated materials, first principles approaches tend to predominate because they rely on a minimum of model assumptions, and are often predictive. This is not the case when correlations are strong because standard methods, usually based on extensions of density functional theory (DFT), lack the sophistication to encapsulate the strong spin and charge fluctuations, or the fidelity to characterize one-particle properties near the Fermi level (which are essential to capture low-energy excitations characteristic of correlated systems); nor are they adequately equipped to generate the (two-particle) susceptibilities.

Low-order many-body perturbation theory, for which the GW approximation is the leading diagram, is usually evaluated as a perturbation relative to a reference system (most commonly DFT), and it is sometimes called G₀W₀. G₀W₀ uses a higher-order theory to improve on the reference low-order Hamiltonian, and in that sense it is similar to the embedding approach. These two approaches improve on the reference in different ways — one as a weak nonlocal perturbation, the other as a nonperturbative but local correction — and are used for different purposes. Nevertheless both methods depend on the reference, which may be arbitrarily constructed, there is ambiguity in the result. In this sense, both are “second principles” methods. Fig. 1 shows how the choice of reference affects physical properties for transition metal (TM) atoms and TM-O dimers; thus even though G₀W₀ is generally regarded as a “first principles” method, it has a second principles flavor.

The self-energy Σ, together with the noninteracting part, determines the one-body Green’s function G, and thus properties derived from it. The success of second-principles methods, is commonly measured by the quality of Σ which is either a function of energy or momentum or both. Its quality is assessed by comparing against observables that are derived from G such as those in Fig. 1. However, Σ alone is not an adequate measure of the theory, and it is the primary aim of this post to establish contexts where it is not adequate.

Need for charge self-consistency

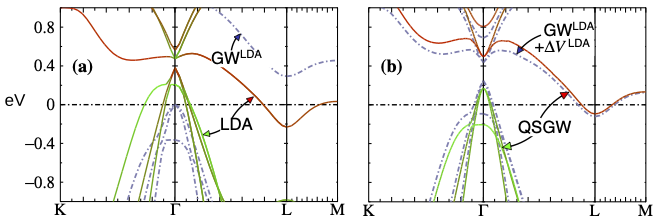
FIG 2. Energy bands of the undistorted P3m1 structure.
(a) Solid lines are LDA results, with red and green depicting a projection onto Ti and Se orbital character, respectively. Blue dashed line shows bands calculated from LDA-based G₀W₀.
(b) Blue dashed line shows bands with same self-energy as in panel (a), with an extra potential ΔV^LDA deriving from a density shift computed from the rotation of the LDA eigenvectors from caused by the difference between the the LDA exchange correlation potential and Σ. Solid lines are results from the Quasiparticle Self-Consistent GW approximation, with the same color scheme as in panel (a). Taken from Ref. 5.

The first example addresses the feedback from the interacting part of G on the noninteracting part, reported in a recent work⁵. Σ should, in principle, modify the electronic eigenfunctions and thus change the real space charge distribution, which changes in turn the noninteracting part of G. Making comparison to experiment while neglecting this implicitly assumes any change in observables relative to the reference originates from Σ alone. Ref. 5 describes two materials systems, TiSe₂ and CrBr₃, where this is not the case. The feedback from charge self-consistency on the noninteracting part from Σ is key in driving qualitative changes to the final electronic structure of these materials.

TiSe₂ is a layered diselenide compound with space group P3m1. Below 200 K, it undergoes a phase transition to a charge-density wave (CDW), forming a commensurate 2 × 2 × 2 superlattice (P3c1) of the original structure. A number of works have tried to determine the energy dispersion around the Fermi level in both phases with a special focus on the gap (whether positive or negative) between the Se-4p valence band at Γ and the Ti-3d conduction band at L (Fig. 2). For P3m1 there is no consensus whether the gap is positive or not, though there is a consensus that the low-temperature CDW (P3c1) phase, has small, positive gap (~100-150 meV).

An LDA+U calculation⁶ yielded 14 meV in the P3m1 phase and 200 meV in the CDW phase. LDA+U is a kind of “second-principles” method because the answer depends U, which is not known. An LDA-based G₀W₀ calculation⁷ yielded a positive (200 meV) gap in the P3m1 phase.

Ref. 5 repeated the LDA-based G₀W₀ calculation (G_LDAW_LDA) of Ref. 7 and found a similar result (Fig. 2a). However, as Ref. 5 shows, the positive gap is an accident of the G_LDAW_LDA perturbative approach: when changes in the density are taken into account, the Γ-L gap becomes negative as in the LDA (Fig. 2b), even while the direct gap at Γ is “positive” (i.e. Ti(d) lies above Se(p)), whereas the LDA gets the topology wrong. It is rather remarkable that the Quasiparticle Self-Consistent GW (QSGW) result looks strikingly similar to G_LDAW_LDA + ΔV^LDA. (Here  ΔV^LDA is an approximate correction to G_LDAW_LDA  originating from modification to the one-body potential causes by rotation of the eigenfunctions.) This indicates that self-consistency doesn’t modify Σ too much; rather, most of the changes self-consistency brings modify the Hartree potential from density changes. TiSe₂ is rather unusual: typically self-consistency tends to increase the bandgap relative to G_LDAW_LDA, because the LDA gap is too small, making W too small.

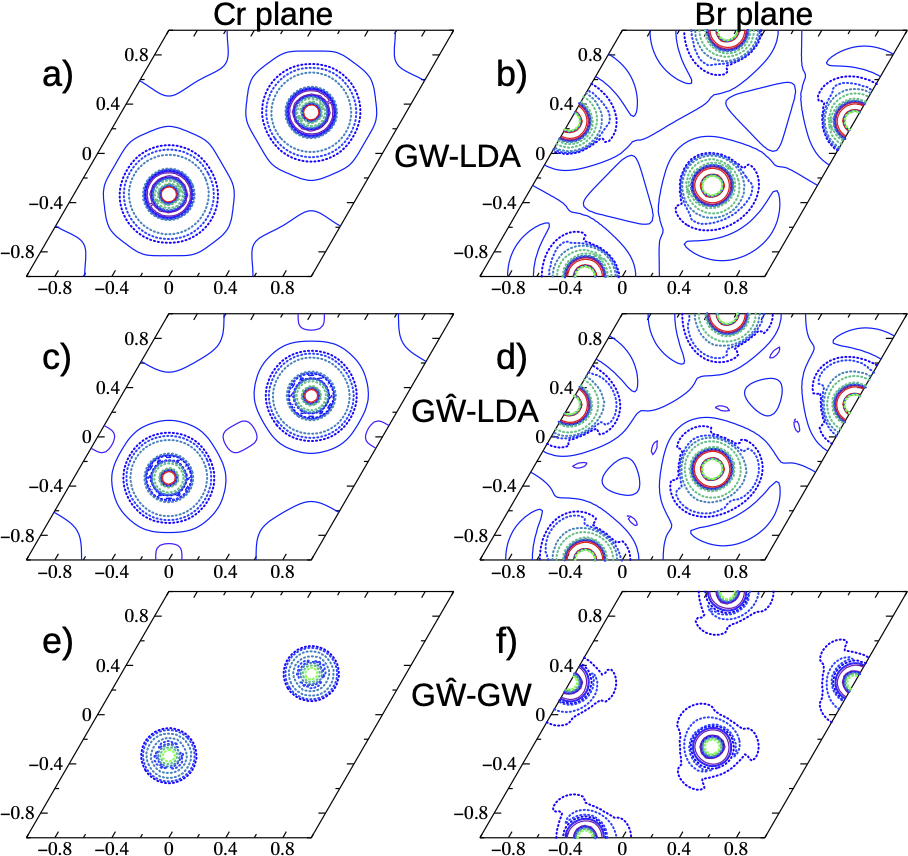
FIG 3. Real-space charge densities (ρ) of CrBr₃ of the highest valence band state with the abscissa and ordinate x and y. All the left panels (a, c, e) pass through a Cr plane and right panels (b, d, f) pass through a Br plane. Panels (a, b) display constant-amplitude contours for QSGW ρ after subtracting out the LDA ρ. Contours are taken in half-decade increments in ρ, with a factor of 300 between highest contour (red) and lowest (blue). Panels (c, d) show the change in ρ passing from LDA to QSGW eigenfunctions; panels (e, f) show the corresponding change passing from QSGW to QSG&#372. In the bottom four panels (c–f), blue → red has a similar meaning as in the top panels (increasing positive δρ), while contours of negative δρ are depicted by increasing strength in the change blue → green.

Excitons in CrBr₃

Self-energy effects in CrBr₃ also modify the band structure. We compared QSGW to density-functional theory, also to QSGW with a ladders added to W (W→Ŵ). The QSGW density is significantly different from the LDA one, but remarkably the addition of higher order ladder diagrams also modifies the density, not just the the quasiparticle spectrum. The density change modifies the one-body part of the potential, which in turn affects the shape of the valence band, including the position of the valence band maximum.

Rotation of eigenfunctions also has a significant effect on those at the band edges, changing their orbital character. This affects the exciton structure, and how the excitons respond to applied fields. This will be taken up in a later post.

Self-Consistency in Σ : CoPS₃ as a case study

To be completed

Intercalated FeSe: how the vertex is essential to understand superconductivity

To be completed

References

¹ R.M. Martin, Electronic Structure (University Press, Cambridge, 2004)

² J.B. Neaton, M.S. Hybertsen, S.G. Louie, Phys. Rev. Lett. 97, 216405 (2006).

³ F. Bruneval, N. Vast, L. Reining, M. Izquierdo, F. Sirotti, N. Barrett, Phys. Rev. Lett. 97, 267601 (2006).

⁴ (Questaal’s methods paper) Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Comp. Phys. Comm. 249, 107065 (2020).

⁵ Swagata Acharya, Dimitar Pashov, Alexander N. Rudenko, Malte Rösner, Mark van Schilfgaarde, Mikhail I. Katsnelson ``Importance of charge self-consistency in first-principles description of strongly correlated systems,’’ npj Comput. Mater 7, 208 (2021).

⁶ Bianco, R., Calandra, M. & Mauri, F. “Electronic and vibrational properties of TiSe₂ in the charge-density-wave phase from first principles,” Phys. Rev. B 92, 094107 (2015)

⁷ M Cazzaniga, at al “Ab initio many-body effects in TiSe₂: a possible excitonic insulator scenario from GW band-shape renormalization,” Phys. Rev. B 85, 195111 (2012)

⁸ M Wu et al., “Physical origin of giant excitonic and magneto-optical responses in two-dimensional ferromagnetic insulators,” Nature communications 10.1 (2019): 1-8; M. Wu, Z. Li, & S. G. Louie, “Optical and magneto-optical properties of ferromagnetic monolayer : a first-principles GW and GW plus Bethe-Salpeter equation study,” Phys. Rev. Mater. 6, 014008 (2022).