Origins of Superconductivity in FeSe

More than a half century passed before phonon mediated superconductivity was finally explained by Bardeen, Cooper and Schrieffer. Then came the high-T_c superconductors in mid 1980’s, and now almost four decades have passed; yet we understand very little of how such high T_c’s can emerge.

High T_c materials are complicated because many factors play an important role in contributing to superconductivity. Model descriptions are very good at identifying possible low-energy degrees of freedom which are the proximate cause for superconductivity. However they cannot take adequate account of the chemistry — the high-energy degrees of freedom that modify the low-energy ones. Equally important, driving forces that cannot be encapsulated in a one-particle description are exceedingly difficult for models to capture. Vertices in spin and charge channels that govern the two-particle properties provide an excellent instance of this difficulty.

In a series of three papers (Refs 1-3), Acharya and coworkers used Questaal’s new implementation joining Quasiparticle Self Consistent GW (QSGW) and Dynamical Mean Field Theory (DMFT) theory⁴ to answer the following questions about FeSe from an ab initio perspective:

1. What role does nemacity play in affecting the spin susceptibility and superconductivity¹?

2. Why does T_c in FeSe increase so dramatically when intercalated with alkali elements²?

3. Why does T_c of FeSe in monolayer form (on a SrTiO₃ substrate) increase by roughly eight-fold compared to the bulk³?

Ab initio theories have historically proved of limited use for unconventional superconductivity, because their fidelity is insufficient capture the subtle and competing many-body effects driving unconventional superconductivity, or other instabilities. The superior fidelity of QSGW+DMFT has radically changed the situation. Combined with a vertex from the two-particle Green’s function, the q- and ω-dependent spin and charge susceptibilities χ^m(q,ω) and χ^d(q,ω) can be calculated. As a final step, the particle-particle vertex generated from χ^m(q,ω) and χ^d(q,ω) via another BSE provides a means to construct an Eliashberg-like equation for instability to superconductivity. This four-tier method is described in some detail in Ref 5, with an application to Sr₂RuO₄, as well as in Refs 2,3. The primary challenge for such a theory is to reliably compute two-particle vertex functions in different channels and identify the primary mechanism for superconductivity.

Nemacity and Superconductivity

It is known that FeSe undergoes a transition from a tetragaonal to orthorhombic phase at 90 K. The transition is not large; the ratio of lattice parameters b/a changes from 1 to 0.98. Nevertheless this induces a striking asymmetry (nematicity) in a number of observed properties: for example d_xz and d_yz bands forming the electron pockets at M are no longer degenerate, as well as the spin susceptibility from neutron measurements. The bare fact of nematicity has led to a great deal of speculation first, about the mechanism responsible for it, and second, its effect on superconductivity. In particular, since the superconductivity is connected to the electron pockets at M (and the hole pockets at Γ), there is speculation that nematicity affects the superconducting state. (For a discussion, see Ref 1 and the references therein.)

As to the first issue, our QSGW+DMFT finds nematicity, but it underestimated. The two likely reasons for this are spin fluctuations or the electron-phonon interaction (or something connected with nuclear displacements.) Whatever the cause, much of the driving force is likely to originate from a nonlocal vertex, absent in both QSGW and DMFT. To address the second issue we mimic the true nematicity by increasing b/a until the asymmetry in electron pocket matches quantum oscillation measurements.

The paper’s primary focus is the second issue, namely what is the effect of nematicity on superconductivity? Since T_c (9  K) is much lower than the transition to the orthorhombic phase (99  K), this is a difficult question to answer experimentally. With the computational machinery at hand, however, we can well answer this question, subject to the caveat that our proxy for obtaining the correct nematicity is also a sufficient proxy for the true effective potential.

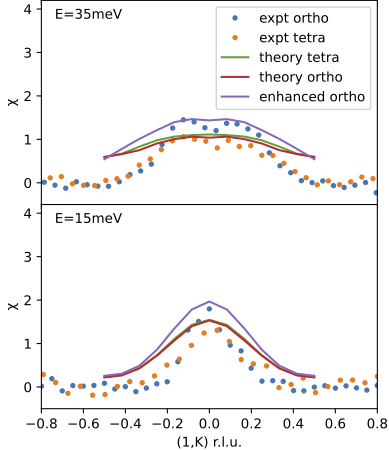
The spin susceptibility was used as a benchmark of the theory, in part because it has been well characterized, but also it is a primary mechanism driving superconductivity in FeSe. Fig. 1 compares calculations with and without nematicity to neutron data. Agreement is good; note in particular how the predicted enhancement in χ^m(q,ω) from nemacity correlates with the experimental data.

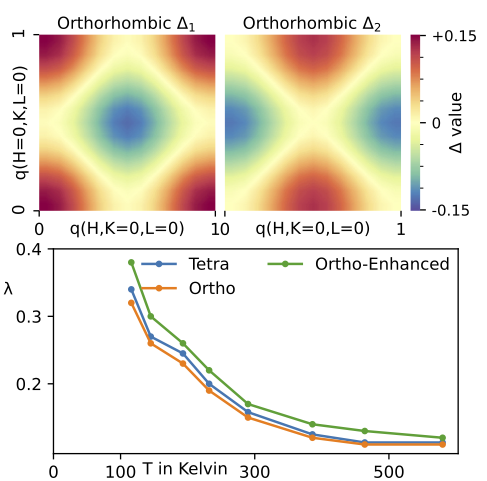
Fig 2 shows that even while χ^m is significantly affected by nemacity, superconductivity is little affected. This is because it is controlled mostly by the d_xy channel, which nemacity hardly effects. The theory predicts that leading instability (top left panel of Fig 2) is of the form Δ₁ ∼ cos(k_x) + cos(k_y), consistent with the s⁺−s⁻ form factor widely expected for FeSe. Note the theory also predicts a weaker (lagging) instability (Δ₂), which is not seen because (Δ₁) is stronger.

In the second paper², the two-particle origin of superconductivity is emphasized. This is important, because the standard BCS and Bose Einstein Condensate (BEC) theories widely invoked to explain superconductivity emphasize the role of one-particle properties, e.g. density-of-states at the Fermi level, D(E_F). In BCS theory T_c has an exponential dependence on D(E_F), while in BEC theory it has a power law dependence. For electron-phonon mediated (conventional) superconductors, T_c does typically increase with D(E_F), and it also does for some (unconventional) cuprate superconductors.

It has been known for some time that when FeSe is intercalated, T_c is enhanced by roughly 4-5 times over the bulk, for many kinds of intercalated variants. Yet DFT calculations show no significant change of D(E_F) on intercalation (and the result is similar when higher level of theory is used). Thus it seems clear that standard application of BCS and BEC theories do not explain the phenomenon, and what leads to such dramatic enhancement in T_c remains unanswered. It is not totally unexpected since even in the BCS theory the constant λ determining T_c is the product of D(E_F) and the effective inter-electron interaction, and the primary reason why common attention is focused on D(E_F) is that it is much easier to calculate. This simplification can miss out on the essential physics, and as we will show here, intercalated FeSe is a very clear example where all the essential changes happen in the effective interaction only. In a more formal language, this effective interaction is nothing but the vertex, which is an essentially two-particle characteristic of correlated systems.

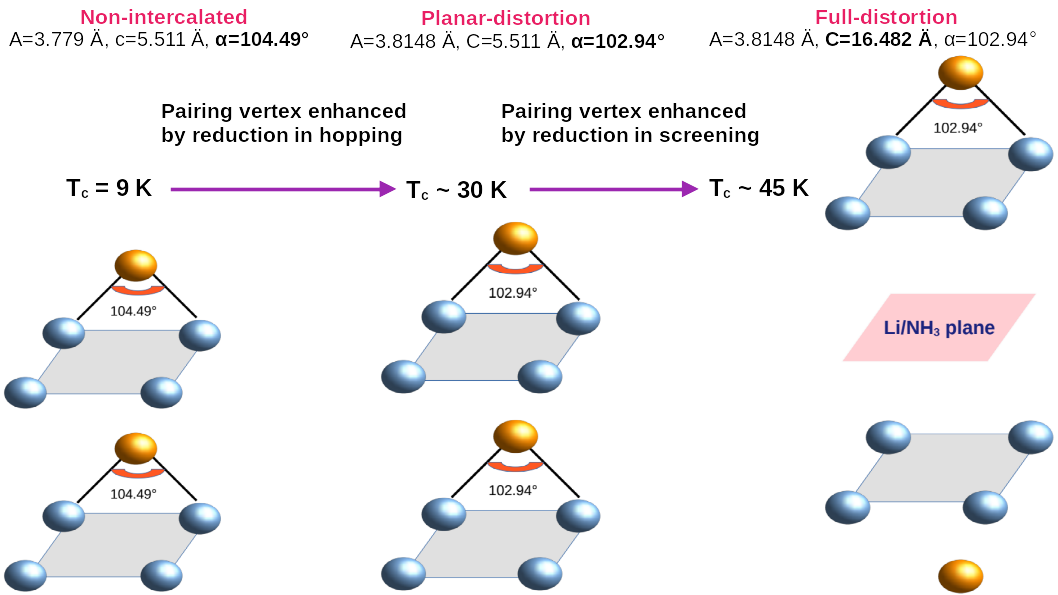
The first task is to establish whether Questaal’s ab initio four-tier QSGW+DMFT theory yields the observed increase in T_c. In addition to doping the system (which as noted, seems not to be significant for FeSe), intercalation modifies the underlying FeSe lattice in two significant ways: it changes the Fe-Se-Fe bond angle (planar-distortion, which we denote as p-d), and it also increases the c axis, changing separation between Fe planes. In what follows, f-d denotes what happens when both effects are taken into account. As Fig 3 shows, the theory predicts that both effects enhance T_c. In both cases, it is driven by an enhancement correlations from the vertex, but for different reasons. In the  p-d  only case, the smaller Fe-Se-Fe bond angle that reduces the Fe-Se-Fe hopping and makes Fe 3d states more correlated. In the  f-d  case, correlations are enhanced because the increased c-axis reduces electronic screening.

When both effects are taken into account, the theory predicts a five-fold enhancement in T_c, dovetailing nicely with measurements on a number of systems with different intercalation elements. The reader is referred to Ref 2 for a detailed analysis for why this happens, but in brief the theory enables us to draw several important conclusions.

First, the one-body properties, e.g. D(E_F), do not account for the enhancement in T_c (Fig 4).

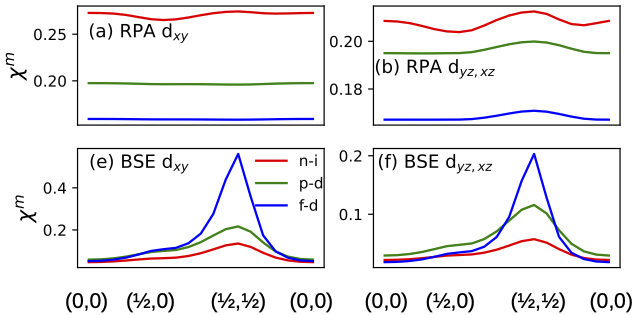
Second, the vertex plays a central role (Fig 5). Without vertex corrections the momentum dependence of χ^m(q) is rather weak and there is no clear separation between χ^m at q=0 and q=(1/2,1/2). Experimentally, in bulk FeSe magnetic fluctuations at q=0 are rather weak compared to the main instability at q=(1/2,1/2) and it is the vertex that brings in the needed momentum dependent variation in χ^m.

Third, superconductivity is predominately driven by the d_xy channel in intercalated FeSe as it does in pristine FeSe¹.

Monolayer FeSe

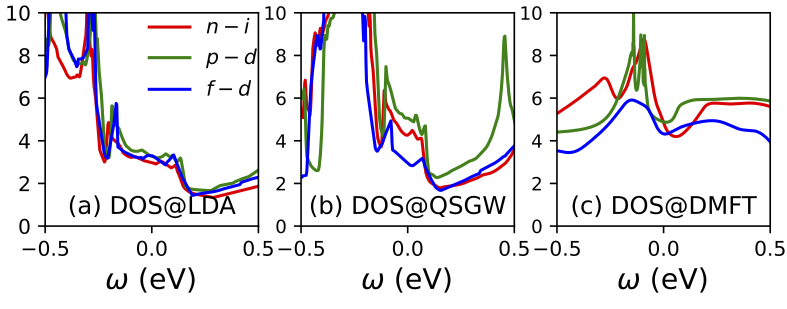
Iron-pnictogen and iron-chalcogen based superconductors are classed as Hund’s metals, meaning correlations mostly originate from the Hund’s exchange parameter J. In recent years a consensus has evolved that strong Hund’s correlations drive the ubiquitous bad metallicity observed in their phase diagrams. Such metals have a multiplicity of bands near the Fermi level E_F; in particular FeSe has all five Fe d states active there. Correlations are observed to be highly orbital-selective (a signature of ``Hundness’’) with d_xy the most strongly correlated orbital. However, very little is known whether Hund’s correlation can generate glue for superconducting pairing and control T_c.

Also, rather remarkably, the bulk T_c (9 K), has been observed to increase to ~75 K when grown as a monolayer on SrTiO₃ (M-FeSe/STO), and 109 K on doped SrTiO₃. Thus while ``Hundness’’ has been found to be important in controlling the single- and two-particle spectral properties of bulk FeSe, the multiplicity of factors (orbital character, spin-orbit coupling, shape of Fermi surface and dispersion of states around it, differences in susceptibilities, nematicity, electron-phonon interaction) obfuscate to what extent Hundness, or other factors, drive superconductivity, and whether `Hundness’ can at all explain the jump in T_c going from bulk to M-FeSe/STO.

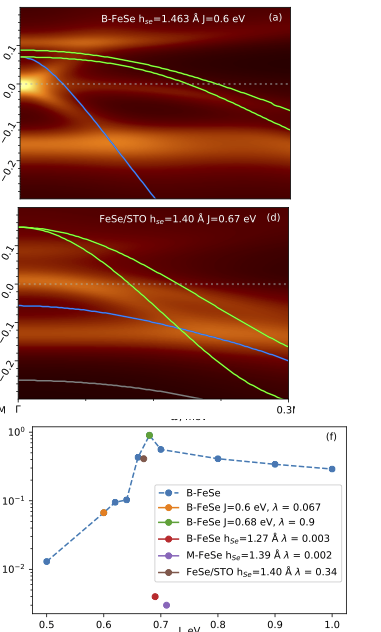
The third paper³ shows that Hundness does explain much of the origins of superconductivity in FeSe. We show explicitly the connections between correlations in d_xy and the superconducting critical temperature T_c. Starting from the ab initio results as a reference, we consider various kinds of excursions in parameter space around the reference to determine what controls T_c. We show small excursions in J can cause colossal changes in T_c. Additionally we consider changes in hopping by varying the Fe-Se bond length in bulk, in the free standing monolayer M-FeSe, and M-FeSe on a SrTiO₃ substrate (M-FeSe/STO). The twin conditions of proximity of d_xy to E_F, and the strength of J emerge as the primary criteria for incoherent spectral response and enhanced single- and two-particle scattering that in turn controls T_c. Using constrained RPA, we show further that FeSe in monolayer form (M-FeSe) provides a natural mechanism to enhance J. These factors thus explain why T_c increases so dramatically for M-FeSe/STO, whereas an isolated monolayer, M-FeSe, is predicted to have a vanishingly small T_c.

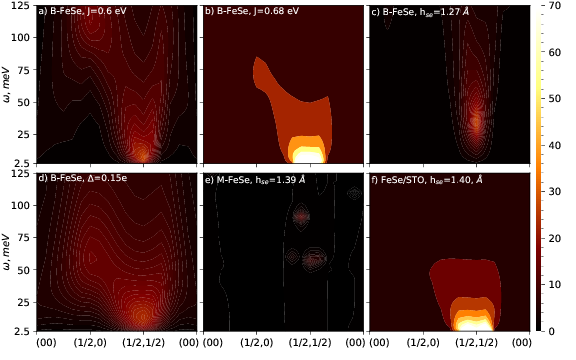
Fig. 7 highlights how the twin effects of J and proximity of the Fe d_xy state to E_F work in concert to govern the intensity of Im χ^m in the vicinity of q=(1/2,1/2,0) and ω=0. Panels (a) and (b) differ only in that J=0.60 eV in the former case (the value computed from constrained RPA) and J artificially increased to 0.68 eV in the latter case: T_c is predicted to be enhanced by roughly a factor of 10. Panels (a) and (c) use the ab initio value for J, but in (c) the Se height is reduced. The intensity of Im χ^m is softened, and the peak lifted well above ω=0. Panel (e) shows Im χ^m for a free-standing monolayer. Once again Im χ^m is very weak and for panels (c) and (e) T_c is very small (see bottom panel of Fig. 6). These are the two instances where d_xy is submerged well below E_F. Finally Im χ^m for m-FeSe/SrTiO₃ is depicted in the bottom right panel (f). O p orbitals in SrTiO₃ couple to the Fe d_xy and push it up, close to E_F. Also because screening is reduced, J increases to 0.67 eV, inducing a strong peak in Im χ^m. These are the two most favorable conditions for high T_c.

References

¹ Swagata Acharya, Dimitar Pashov, Mark van Schilfgaarde, Role of nematicity in controlling spin fluctuations and superconducting Tc in bulk FeSe, Phys. Rev. B 105, 144507 (2022).

² Swagata Acharya, Mikhail I. Katsnelson, Mark van Schilfgaarde, Vertex dominated superconductivity in intercalated FeSe, Preprint https://doi.org/10.48550/arXiv.2205.14422.

³ Swagata Acharya, Dimitar Pashov, Francois Jamet, Mark van Schilfgaarde, Electronic Origin of Tc in Bulk and Monolayer FeSe, Symmetry 13, 169 (2021).

⁴ Dimitar Pashov, Swagata Acharya, Walter R. L. Lambrecht, Jerome Jackson, Kirill D. Belashchenko, Athanasios Chantis, Francois Jamet, Mark van Schilfgaarde, Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique, Section 7, Comp. Phys. Comm. 249, 107065 (2020).

⁵ Swagata Acharya, Dimitar Pashov, Elena Chachkarova, Mark van Schilfgaarde, and Cedric Weber, Electronic structure correspondence of singlet-triplet scale separation in strained Sr₂RuO₄, Appl. Sci. 11, 508 (2021). https://www.mdpi.com/2076-3417/11/2/508.

⁶ Q. Wang et al, Nat. Commun. 7, 12182 (2016).