Examples
An embedding scheme within the Quasiparticle Self-consistent GW approximation
The quasiparticle self-consistent (QS) GW approximation offers a high-fidelity alternative to Kohn-Sham density functional theory (DFT) for obtaining quasiparticle energies from their eigenvalues by means of an energy-independent and Hermitian self-energy.
Nonetheless, GW theory has not yet found widespread applications in defect studies. This is at least in part due to the large computational effort required for GW calculations. In particular, the latter is challenging for the large supercells needed to represent defects adequately. Thus, there is a need for improving the efficiency of the GW approach, eventually at the cost of some simplification, to make it applicable to larger systems, or systems without periodic boundary conditions.
Our goal with this project, (published recently in Phys. Rev. B) was to explore whether the GW self-energy of a defect system could be constructed from that of the host and the defect site itself or its immediate neighborhood without having to carry out the expensive full GW calculation for the large unit cell required to adequately represent a defect.
Typical defect calculations of today employ semi-local generalized gradient approximation (GGA) or local density approximations (LDA). The infamous gap underestimate of these approaches can lead to serious errors in defect calculations. Defect levels, which should be in the gap may end up in the band continuum. This also affects the total energies and therefore transition levels if one considers charge states in which that defect level (now a resonance in the band) is given an extra charge because in the calculation that charge is actually placed in a delocalized state at the bottom of the band rather than in the defect level. This can be partially resolved with mixed functionals, nonlocal functionals such as the HSE functional of Scuseria et al or LDA+U, or the NLEP scheme of Lany and Zunger, but there are inevitable ambiguities. Such functionals are tuned to work for particular systems, but all of them are essentially ad hoc extensions of DFT to reproduce a few properties. None has the rigorous formal structure or consistently high fidelity of QSGW.
In this paper, we showed that when the QSGW self-energy can be expanded in a basis of atom-centered orbitals, such as the linearized muffin-tin orbitals (LMTO), that are sufficiently localized (meaning their range is less than that of the self-energy), then the self-energy matrix can be represented in real space within a finite range. This then offers new opportunities to approximately construct the self-energy of a system by partitioning the system in sub parts and constructing the self-energy by a cut-and-paste approach. In particular, we apply this here to point defects. We first construct the self-energy of the host in a supercell from that of the primitive cell. In a second step, we replace the part of the self-energy matrix related to the defect atom and its near neighborhood in terms of the self-energy of a smaller supercell containing the defect for which a GW calculation is more readily feasible. We then validate the accuracy of the approach with various examples.
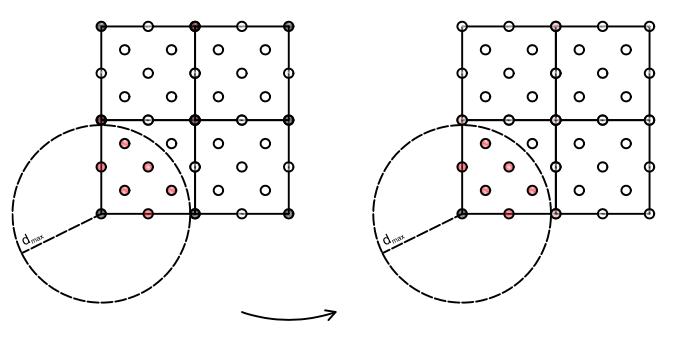 FIG 1: Schematic illustration of the self-energy editor cut-and-paste method. The left shows the supercell with defect atoms shown as black spheres and host atoms as open circles and the atoms within a range from the defect atom indicated by the dashed circle are red. The target system with 1 defect is shown on the right. In this example, we assume only the defect atom itself comprises the defect region and the atoms within the range contribute to the self-energy in real space. The self-energy of the atom pairs corresponding to the red atoms connected to the defect atom in the target cell are replaced by those from the supercell, shown on the left.
FIG 1: Schematic illustration of the self-energy editor cut-and-paste method. The left shows the supercell with defect atoms shown as black spheres and host atoms as open circles and the atoms within a range from the defect atom indicated by the dashed circle are red. The target system with 1 defect is shown on the right. In this example, we assume only the defect atom itself comprises the defect region and the atoms within the range contribute to the self-energy in real space. The self-energy of the atom pairs corresponding to the red atoms connected to the defect atom in the target cell are replaced by those from the supercell, shown on the left.
One important advantage of this method is that once the full QSGW calculation for the small cell is made, moving to larger host cells and calculating the defect properties in the dilute limit is a straightforward procedure and one can achieve GW-level accuracies for the cost of an LDA calculation for even larger cells. Although we do not include the exact calculations for these larger cells in this work, we analyze a 216 atom cell, i.e. a 3×3×3 supercell of the conventional simple cubic 8 atom cell. In such a cell the dispersion of the defect band is almost zero, indicating we are close to the dilute limit. Furthermore, this allows us to better evaluate the nature of the defect band dispersion. As mentioned earlier, the top of the defect band which is flat between X and M remains the same as in the smaller 64 and 32 atom cells but the band width is reduced at Γ. This helps us to identify the top of the defect band with the dilute limit defect level.

FIG. 2 shows the DOS of a 128 atom cell, half the size of the largest cell considered in this work, which widen the neutral EL2 defect level to about 0.5 eV. The center of gravity remains unchanged, so the 128 atom cell is adequate to identify the level position.
As shown in the figure, relaxation of the lattice around the cell has a non-negligible effect, shifting the EL2 by about 0.3 eV.
| Potential | QSGW | 80%QSGW+20%LDA | ||
|---|---|---|---|---|
| structure | EL2 | gap | EL2 | gap |
| unrelaxed | 1.13 | 1.69 | 1.02 | 1.44 |
| relaxed | 0.83 | 1.68 | 0.74 | 1.42 |
The Table shows the band center of neutral EL2 defect, in eV, relative to the valence band maximum, embedded in a 128 atom cell. Two calculations are shown: the first allowing no lattice relaxation, and the second including it. QSGW is well known to slightly overestimate gaps in semiconductors3. This is because of the omission of ladder diagrams in the RPA, and if they are included in the screened coulomb interaction W the overestimate becomes very small or even slightly negative4. It is possible to include them, but the correction is not large. A simpler semi-empirical approach is to take a hybrid of 80% QSGW and 20% LDA. The hybrid approach was systematically studied by Deguchi et al. in sp semiconductors and found to be quite reliable.5
The Table shows both straight QSGW results and hybrid results. In both cases, the EL2 falls almost exactly at midgap (0.8 eV for QSGW, 0.7 eV for the hybrid case). Experimentally, it is known to fall at midgap, at 0.7 eV. Thus when relaxations are taken into account, the theory predicts the position of EL2 with the same fidelity as it does periodic systems3.
1 S. Lany and A. Zunger, “Magnetic interactions of Cr−Cr and Co−Co impurity pairs in ZnO within a band-gap corrected density functional approach,” Phys. Rev. B 77, 241201 (2008)
2 Jochen Heyd and Gustavo E Scuseria, J Chem Phys 1187, “Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional,” J. Chem. Phys. 121, 1187 (2004)
3 M. van Schilfgaarde, Takao Kotani, S. V. Faleev, “Quasiparticle self-consistent GW theory,” Phys. Rev. Lett. 96, 226402 (2006). http://link.aps.org/abstract/PRL/v96/e226402
4 Brian Cunningham, Myrta Gruening, Dimitar Pashov, Mark van Schilfgaarde, “QSGW: Quasiparticle Self consistent GW with ladder diagrams in W,” Preprint https://arxiv.org/abs/2106.05759
5 Daiki Deguchi et al, “Accurate energy bands calculated by the hybrid quasiparticle self-consistent GW method implemented in the ecalj package,” Jpn. J. Appl. Phys. 55 051201 (2016). https://iopscience.iop.org/article/10.7567/JJAP.55.051201
PAPERS · EMBEDDING · DEFECTS
