Examples

Excitons in Cr{Cl,Br,I}₃

A QSGW description of the electronic structure and excitons in ferromagnetic CrX₃ compounds

In two papers (Refs 1,2) we explore the family of chromium trihalides CrX₃, X=Cl, Br, I. This family has emerged as a new class of magnetic 2D crystals. Ferromagnetism (FM) in a CrI₃ monolayer was first reported in 2017, which was followed by observation of FM in CrBr₃, CrCl₃ and many other compounds as well. The second paper uses an enhanced version of the Quasiparticle Self-consistent GW approximation (QSGŴ) to investigate the role of excitons, as described in second part.

FM is intrinsic to these systems, which distinguishes them from traditional 2D sp-electron magnets where magnetism is induced by proximity to a FM substrate. Long range-order is typically suppressed in two-dimensional magnets, but it can be stabilized by magneto-crystalline anisotropy, which opens an energy gap in the magnon spectra and therefore protects the FM in two dimensions. They have a layered structure and with weak inter-layer van-der-Waals interactions. Thus they are loosely coupled to their substrates, providing greater flexibility in functionalizing them and controlling their properties, e.g. by varying the layer-number or by applying a gate voltage. This offers new possibilities to make spintronic devices with high accuracy and efficiency.

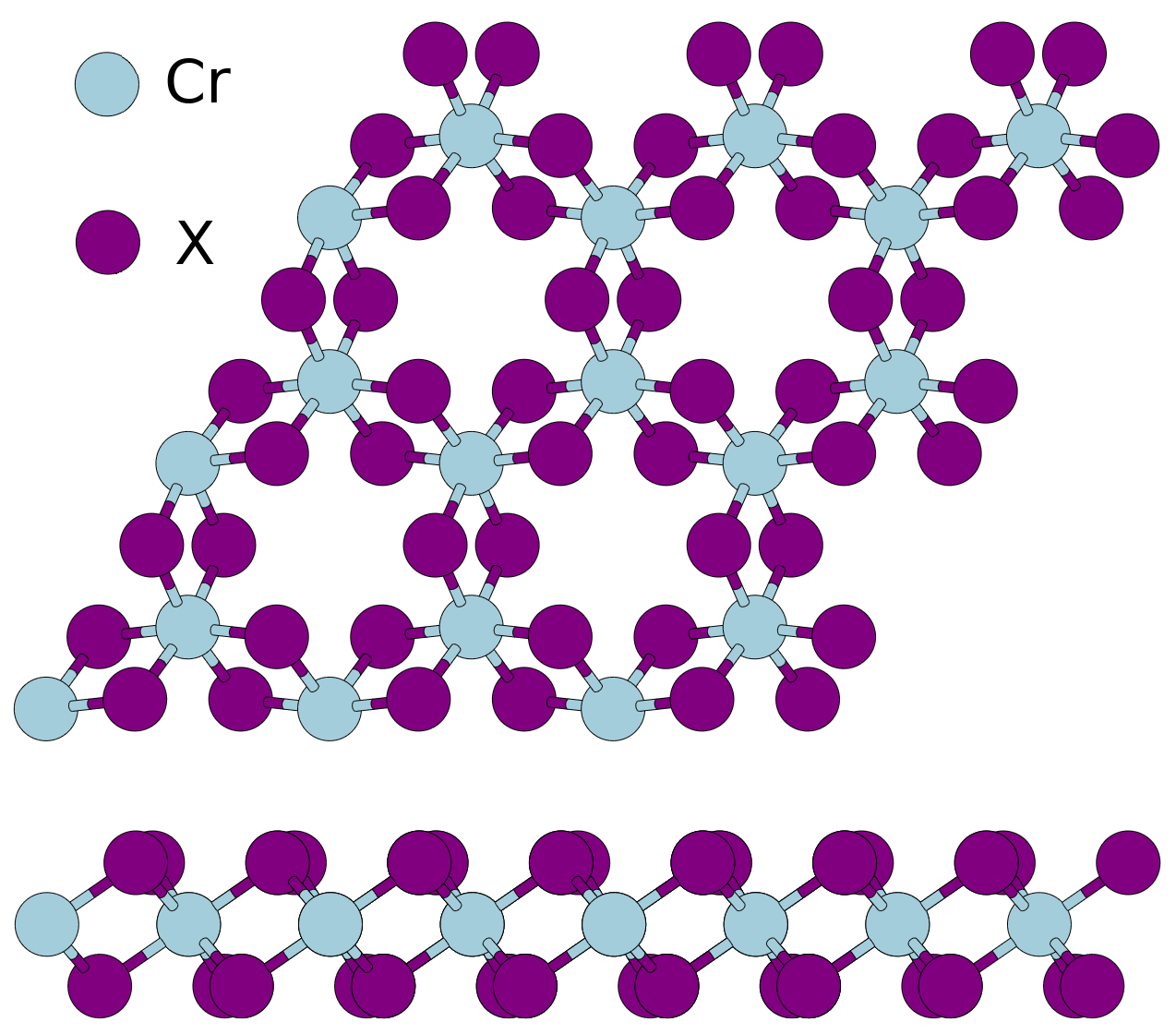
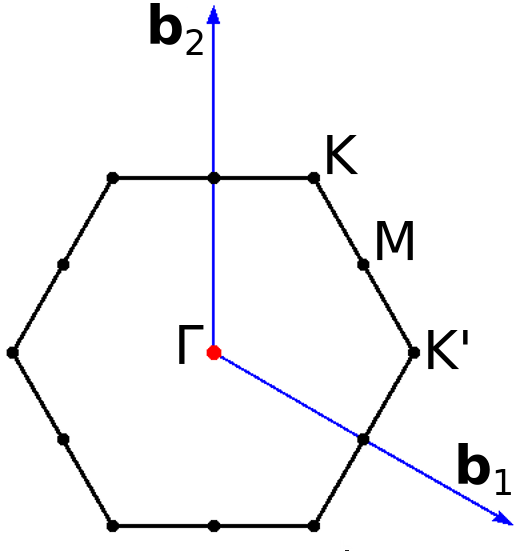
FIG 1 (Left) Ball-and-stick model of the crystal structure of monolayer chromium trihalides CrX₃ (X=Cl, Br, I). (Right) Brillouin zone of the corresponding hexagonal lattice with the high-symmetry points indicated. b₁ and b₂ denote reciprocal lattice vectors.

CrX₃ is a two-dimensional FM insulator with FM originating from the Cr-X-Cr superexchange interaction. Six Cr³⁺ ions form a honeycomb structure, surrounded by six X in an octahedral geometry (see Fig. 1). The shared ligands enables a pathway for Cr-X-Cr superexchange. The ionic model predicts a magnetic moment of 3μ_B on each Cr³⁺ ion.

FIG 2. The density of states projected onto the Cr-d and I-p states at different levels of the theory. Note the striking difference between and the LDA, and how QSGŴ is different from QSGW.

Recent Density Functional Theory (DFT) calculations confirm the qualitative understandings derived from the ionic model. However, at quantitative level details start to differ from the fully ionic picture. The main focus of the first paper¹ analyze at different levels of theory (DFT, self-consistent QSGW and BSE-enhanced QSGW (QSGŴ), allow us to study the roles of self-consistent charge densities and self-energies in determining the key features of the electronic structures at different levels of the theory. This system is a rare case where ladder diagrams have a large effect. Not only do they reduce the gap as is typical³, but they modify the structure of the valence bands, which is not. Many-body effects in both QSGW and QSGŴ enhance the bandgap relative to the LDA, and make the valence band eigenfunctions more directional.

Excitons in CrX₃

In a second paper² we examine excitons in CrX₃ as monolayers (ml) and as bulk.

Their binding is remarkably strong (~2-3 eV), which in the continuum between Frenkel excitons (localized to a site, e.g. the Cr 3d orbital) and delocalized Wannier excitons, should put them firmly in the Frenkel camp. They are thought to emerge from the atomic d−d transitions between the Cr 3d-t_2g and e_g orbitals. The argument is bolstered by the observation that excitons in monolayers have energies very similar to the bulk. The Laporte rule, which restricts such parity forbidden atomic transitions, can relax if, at least, one element is present: spin-orbit coupling, odd-parity phonons or Jahn-Teller distortion. In this paper we show that these excitons in CrX₃, in both its bulk and monolayer variants, have band-origin and do not require the relaxation of Laporte rule as a fundamental principle.

Even while the character of these excitons is mostly determined by the Cr-d orbital manifold, nevertheless, they appear only as a consequence of X-p states hybridizing with the Cr-d. The hybridization enhances as the halogen atom becomes heavier, bringing the X-p states closer to the Cr-d states in the sequence Cl→Br→I, with an attendant increase in exciton intensity and decrease in binding energy.

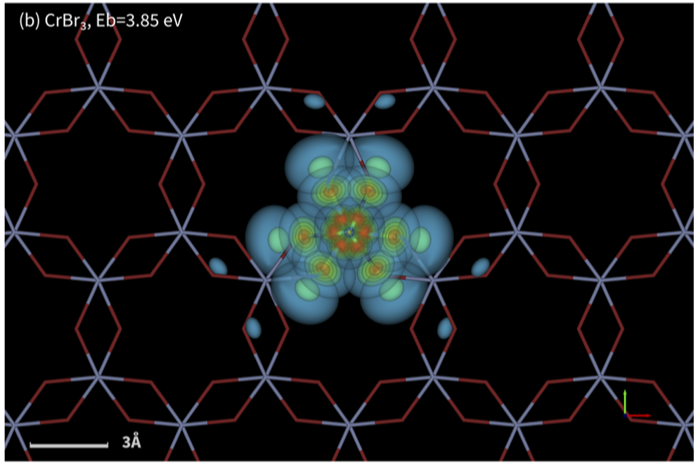
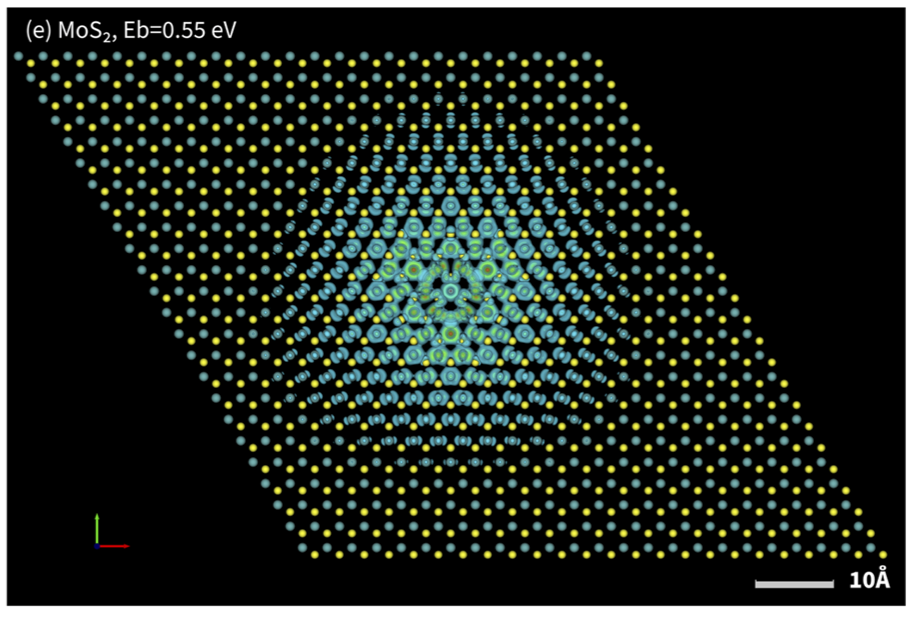
FIG 3. Comparison between the differential reflectivity data combined with low energy photo-luminescence data from the recent experimental work on ml-CrI₃ against our theoretical Imε_xx results. The theoretical spectra for Imε_xx is rigidly blue-shifted slightly as our exciton were by ~0.2 eV too deep compared to experiments. The theoretical data for different optical broadening schemes are also plotted on top of the experimental data.

This paper also depicts some excitons in real space, showing how they are strongly localized around the Cr, but are not confined to it. This is the first demonstration of Questaal’s ability to generate real-space description of excitons.

FIG 4. 3.85 eV exciton in real space in CrBr₃. Shown for comparison is the exciton in a MoS₂ monolayer. The deeper the exciton, the more localized it is, but in contrast to ml-MoS₂ (binding energy 0.55 eV) all excitons CrX₃ are very localized. See Fig. 9 of Ref 2.

¹ See this paper and references therein:
S. Acharya, et al, ``Electronic Structure of Chromium Trihalides beyond Density Functional Theory,’’ Phys. Rev. B 104, 155109 (2021) https://journals.aps.org/prb/abstract/10.1103/PhysRevB.104.155109

² Jochen Heyd and Gustavo E Scuseria, J Chem Phys 1187, ``Real- and momentum-space description of the excitons in bulk and monolayer chromium tri-halides,’’ npj 2D Mater and Applications 6, 33 (2022)

³ Brian Cunningham, Myrta Gruening, Dimitar Pashov, Mark van Schilfgaarde, “QSGW: Quasiparticle Self consistent GW with ladder diagrams in W,” Preprint https://arxiv.org/abs/2106.05759

2022-07-06 PAPERS · MAGNETISM · 2D MATERIALS